摘要(Abstract)
我们先来看看作者的卖点:
Visual place recognition (VPR) is an essential task for multiple applications such as augmented reality and robot localization. Over the past decade, mainstream methods in the VPR area have been to use feature representation based on global aggregation, as exemplified by NetVLAD. These features are suitable for large-scale VPR and robust against viewpoint changes. However, the VLAD-based aggregation methods usually learn a large number of (e.g., 64) clusters and their corresponding cluster centers, which directly leads to a high dimension of the yielded global features. More importantly, when there is a domain gap between the data in training and inference, the cluster centers determined on the training set are usually improper for inference, resulting in a performance drop. To this end, we first att empt to improve NetVLAD by removing the cluster center and setting only a small number of (e.g., only 4) clusters. The proposed method not only simplifies NetVLAD but also enhances the generalizability across differentdomains. We name this method SuperVLAD. In addition, by introducing ghost clusters that will not be retained in the final output, we further propose a very low-dimensional 1-Cluster VLAD descriptor, which has the same dimension as the output of GeM pooling but performs notably better. Experimental results suggest that, when paired with a transformer-based backbone, our SuperVLAD shows better domain generalization performance than NetVLAD with significantly fewer parameters. The proposed method also surpasses state-of-the-art methods with lower feature dimensions on several benchmark datasets. The code is available at https://github.com/lu-feng/SuperVLAD.
文章开篇直指NetVLAD的两个问题:
- 维度太高:通常会聚64个簇,导致最终的全局表征维度太高
- 域间隙(Domain Gap):训练集的中心在测试集上没用(这是这篇论文最大的立足点)
然后作者给出了他的核心卖点:
- 用极少的簇+去中心化的方法总的来说就是加权池化
- 提出1-Cluster VLAD,并利用 Ghost Clusters 实现,以此来打败 GeM Pooling
引言(Introduction)
这里我们只需要看一个图即可
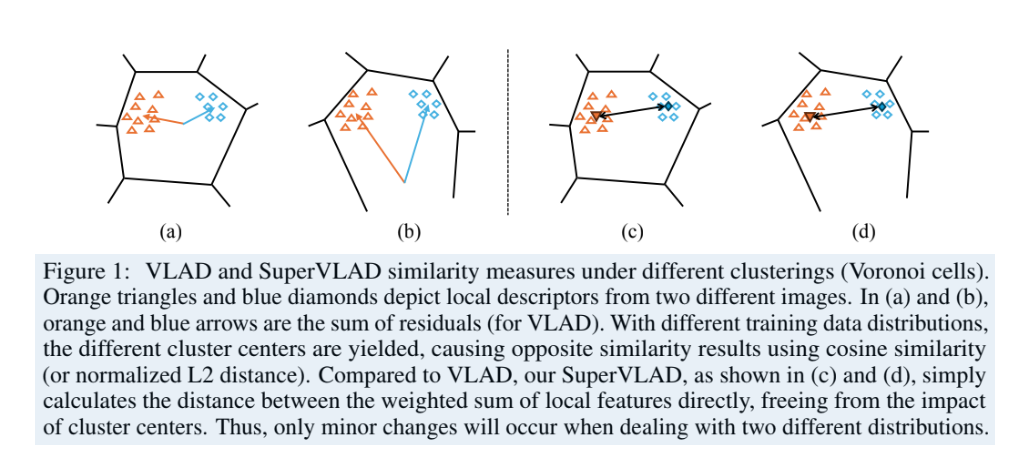
作者画了一个非常直观的 Voronoi 图,也是参考的NetVLAD论文
- 左边(NetVLAD):因为有中心 $c_k$,当数据分布(橙色 vs 蓝色)偏移时,残差向量(箭头)的方向会剧烈变化。
- 右边(SuperVLAD):因为没有中心,直接聚合特征本身,所以对分布偏移不敏感。
点评: 这张图极其重要,它从直觉上说服了审稿人:“少即是多” (Less is More)。
不过,SuperVLAD虽然还叫VLAD,但其中最关键的残差聚合已经消失了,因此叫SuperPooing更加合适。相比NetVLAD,SuperVLAD在intro后半部分的写法就没有那么严丝合缝了,也就是标准的堆砌贡献、实验结论。虽然这种写法是目前顶会上的主流,不过个人还是更喜欢NetVLAD这种经典论文一环扣一环的写法。
方法(Methodology)
我们来回顾NetVLAD的公式:
$$ V _ { k , j } = \sum _ { i = 1 } ^ { N } a _ { k } ( x _ { i } ) ( x _ { i , j } - c _ { k , j } ) $$$$ a _ { k } ( x _ { i } ) = \frac { e ^ { - \alpha | | x _ { i } - c _ { k } | | ^ { 2 } } } { \sum _ { k ^ { \prime } } e ^ { - \alpha | | x _ { i } - c _ { k ^ { \prime } }| | ^ { 2 } } } \\ a _ { k } ( x _ { i } ) = \frac { e ^ { w _ { k } ^ { T } x _ { i } + b _ { k } } } { \sum _ { k ^ { \prime } } e ^ { w _ { k } ^ { T } x _ { i } + b _ { k ^ { \prime } } }} $$而SuperVLAD的公式如下:
$$ V _ { k , j } = \sum _ { i = 1 } ^ { N } a _ { k } ( x _ { i } ) x _ { i , j } = \sum _ { i = 1 } ^ { N } \frac { e ^ { w _ { k } ^ { T } x _ { i } + b _ { k } } } { \sum _ { k ^ { \prime } } e ^ { w _ { k } ^ { T } x _ { i } + b _ { k ^ { \prime } } } x _ { i , j } } $$简而言之就是:
NetVLAD 公式:$V = \sum a (x - c)$
SuperVLAD 公式:$V = \sum a \cdot x$
作者称这为 “First-order statistics of local features”(局部特征的一阶统计量),而不是简单的“加权求和”。听起来就高大上多了,当然这个话术是从VLAD开始就有的,只能说写论文重点还是看怎么写呀!
高光时刻(Highlight)
不过话虽这么说,但是这篇论文能中NIPS这样高质量的会议可不单单是靠这种取巧,除了后面大量的实验之外,在Methodology这里作者还有几个做得非常好的地方:
关键辩护: 作者特意提到这不同于 Attention,其实是个非常关键的地方,需要解释的是作者这里所说的attention应该是 “cross-attention”
“However, for a given cluster, the sum of the weights of assigning all features to it is not fixed (for attention, it is the constant 1).”
在标准 Cross-Attention 中,我们计算 Query (Cluster $k$) 和 Key (Feature $i$) 的相似度分数 $S_{k,i}$。
Softmax 通常是在 Key 的维度(也就是 Patch 数量 $N$) 上进行的(即 Row-wise,如果行是 Cluster):
$$ \alpha_{k,i} = \frac{e^{S_{k,i}}}{\sum_{j=1}^{N} e^{S_{k,j}}} $$物理意义: 对于每一个 Cluster(Query),它在所有 Patch 上的注意力权重之和必须为 1。即每个cluster会投入自己所有的注意力分数,分发到各个patch上。这是一种聚焦机制,而Soft-Assignment是一种 “路由” (Routing) 机制。即patch通过softmax选择将自己的权重(概率)分配给某个簇,如若图像中不存在某类特征,该簇的聚合权重和 $W_k$ 可趋近于 0;若存在大量该类特征,则 $W_k$ 会很大。
第一个这个思考对我个人的启发非常大
1-Cluster VLAD: 想不到吧,我还有contri!
这里在去中心化之后了,其实完全就和加权池化非常类似了,因此这里作者想到,强制把输出压到和输入一样的维度(768维)。
- 对比 GeM Pooling 和 Class Token。将cluster设置为1,那不就是平均池化了吗?特征维度也大大减小。
- 但为了提升性能,这里的关键依然是引入Ghost机制,通过“1个真实簇 + 多个幽灵簇”的竞争机制,比简单的 GeM Pooling 能保留更多关键信息。
Cross-image Interaction
作者借鉴了 CricaVPR(其实也是他自己的工作 ),引入了一个 Batch 内的交互。个人猜测,在sota榜上性能提升最明显的原因也是由于引入了这个 cross image encoder。就DL而言,能100%直观提点的就是更大、更强的模型,更多的数据,更高的计算量和信息量,更先进的训练策略等。而真正对模型的小修小改,或者寻找奇淫巧计只能算蚊子腿了,scaling law还是太权威了。
实验(Experiment)
这篇论文的实验做得非常扎实,尤其是附录部分,不仅有成功的实验,还诚实地放出了失败/受限的实验(关于 CNN 的部分),我们就配合Gemini老师的整理浏览一下~
我们可以把它的实验分为三条线索来梳理:核心假设验证、组件有效性验证、局限性分析(诚实测试)
🟢 线索一:核心假设验证 —— “去中心化”真的好吗?
作者的核心论点是:去掉聚类中心 $c_k$,能减少过拟合,提高跨域(Cross-domain)泛化能力。
- 实验 1:跨域泛化测试 (Table 4)
- 设置: 训练集用 Pitts30k(只有城市),测试集用 MSLS(包含郊区、自然风光)。这是典型的 Domain Gap 场景。
- 结果:
- NetVLAD (CCT Backbone): R@1 = 55.4%
- SuperVLAD (CCT Backbone): R@1 = 62.2% (+6.8%)
- 结论: 在跨域场景下,SuperVLAD 完胜。证明了 NetVLAD 记住的“城市聚类中心”在“自然风光”里确实水土不服。
- 实验 2:同域测试 (Table 4)
- 设置: 训练和测试都在 Pitts30k。
- 结果: 两者分数几乎一样(84.7% vs 84.7%)。
- 结论: 在没有 Domain Gap 时,去不去中心无所谓。这进一步佐证了作者的观点:SuperVLAD 的优势专门在于泛化。
🔵 线索二:组件有效性验证 —— “幽灵簇”和“DINOv2”
- 实验 3:Ghost Clusters 的作用 (Table 5)
- 设置: 对比有无 Ghost Cluster 的模型。
- 结果: 在 CCT Backbone 上,加上 Ghost 后 R@1 从 60.3% 提升到 62.2%。
- 结论: Ghost 确实能吸走噪声。但在 DINOv2 上提升不明显(因为 DINOv2 特征本身已经太强了,噪声很少)。
- 实验 4:1-Cluster VLAD 的极致压缩 (Table 6)
- 设置: 强制把输出压到和输入一样的维度(768维)。对比 GeM Pooling 和 Class Token。
- 结果:
- GeM Pooling: 85.4%
- Class Token: 88.4%
- 1-Cluster VLAD: 90.4%
- 结论: 这是全篇最大的亮点之一。证明了通过“1个真实簇 + 多个幽灵簇”的竞争机制,比简单的 GeM Pooling 能保留更多关键信息。
- 实验 5:与 SOTA 的终极对决 (Table 2)
- 结果: 在 Pitts30k, MSLS, Nordland, SPED 四大金刚数据集上,SuperVLAD 全面超越 NetVLAD, CosPlace, MixVPR, SelaVPR 等对手。
- 意义: 证明了“DINOv2 + SuperVLAD”这套组合拳是目前的版本答案。
🔴 线索三:局限性分析 —— 附录里的“大实话”
作者在附录里放了一些非常有价值的“失败”实验,这在论文中是非常加分的(增加了可信度)。
- 实验 6:CNN 上的滑铁卢 (Appendix C, Table 9)
- 设置: 把 Backbone 换回老旧的 VGG16。
- 结果: SuperVLAD 打不过 NetVLAD。
- NetVLAD (64 clusters): 88.4%
- SuperVLAD (64 clusters): 86.3%
- 深度分析: 作者承认,当特征不够强(CNN 特征)时,NetVLAD 那种记录“残差”(细节纹理差异)的能力非常重要。SuperVLAD 这种“粗暴”的加权求和,只有在特征本身语义极强(Transformer/DINOv2)时才玩得转。
- 实验 7:簇数量的博弈 (Appendix B, Table 8)
- 结果:
- 簇少时(K=2):SuperVLAD 赢 (+8.5%)。
- 簇多时(K=64):NetVLAD 赢。
- 结论: SuperVLAD 适合轻量化。如果你非要搞 64 个簇的大模型,NetVLAD 的中心机制反而能更精细地切分空间。
- 结果:

评论