引言
Scaled Dot-Product Attention (SDPA) 是 Transformer 架构的核心计算单元。这里我摘录了和AI对话的结果,结合个人查阅到的资料,从数学第一性原理出发,严格推导其设计背后的统计学依据、几何直觉和训练动力学。
我们将回答以下关键问题:
- 为什么要除以 $\sqrt{d_k}$? —— 方差稳定性的严格证明
- 为什么选择点积而非其他相似度? —— 计算复杂度与几何意义
- Q 和 K 为什么看起来对称却不能交换? —— 对称性破缺的机制
- 训练过程中权重矩阵如何演进? —— 从随机初始化到语义角色分化
1. 核心公式的分解
Scaled Dot-Product Attention 的完整数学表达式:
$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$符号定义
| 符号 | 形状 | 含义 |
|---|---|---|
| $Q$ | $(n, d_k)$ | Query 矩阵:$n$ 个查询向量,每个维度 $d_k$ |
| $K$ | $(n, d_k)$ | Key 矩阵:$n$ 个键向量,每个维度 $d_k$ |
| $V$ | $(n, d_v)$ | Value 矩阵:$n$ 个值向量,每个维度 $d_v$ |
| $n$ | 标量 | 序列长度(如句子中的词数) |
| $d_k$ | 标量 | Query 和 Key 的向量维度 |
| $d_v$ | 标量 | Value 的向量维度(可以与 $d_k$ 不同) |
计算流程
步骤 1:线性投影生成 Q, K, V
$$ \begin{aligned} Q &= XW^Q \quad \text{其中 } W^Q \in \mathbb{R}^{d_{\text{model}} \times d_k} \\ K &= XW^K \quad \text{其中 } W^K \in \mathbb{R}^{d_{\text{model}} \times d_k} \\ V &= XW^V \quad \text{其中 } W^V \in \mathbb{R}^{d_{\text{model}} \times d_v} \end{aligned} $$其中 $X \in \mathbb{R}^{n \times d_{\text{model}}}$ 是输入嵌入矩阵。下图为Transformer Explainer的可视化效果:
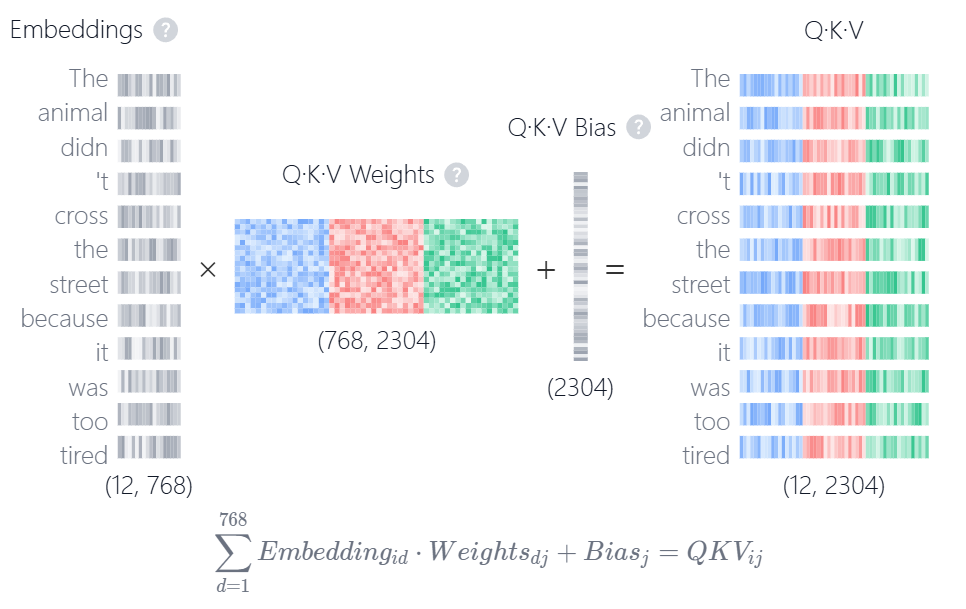
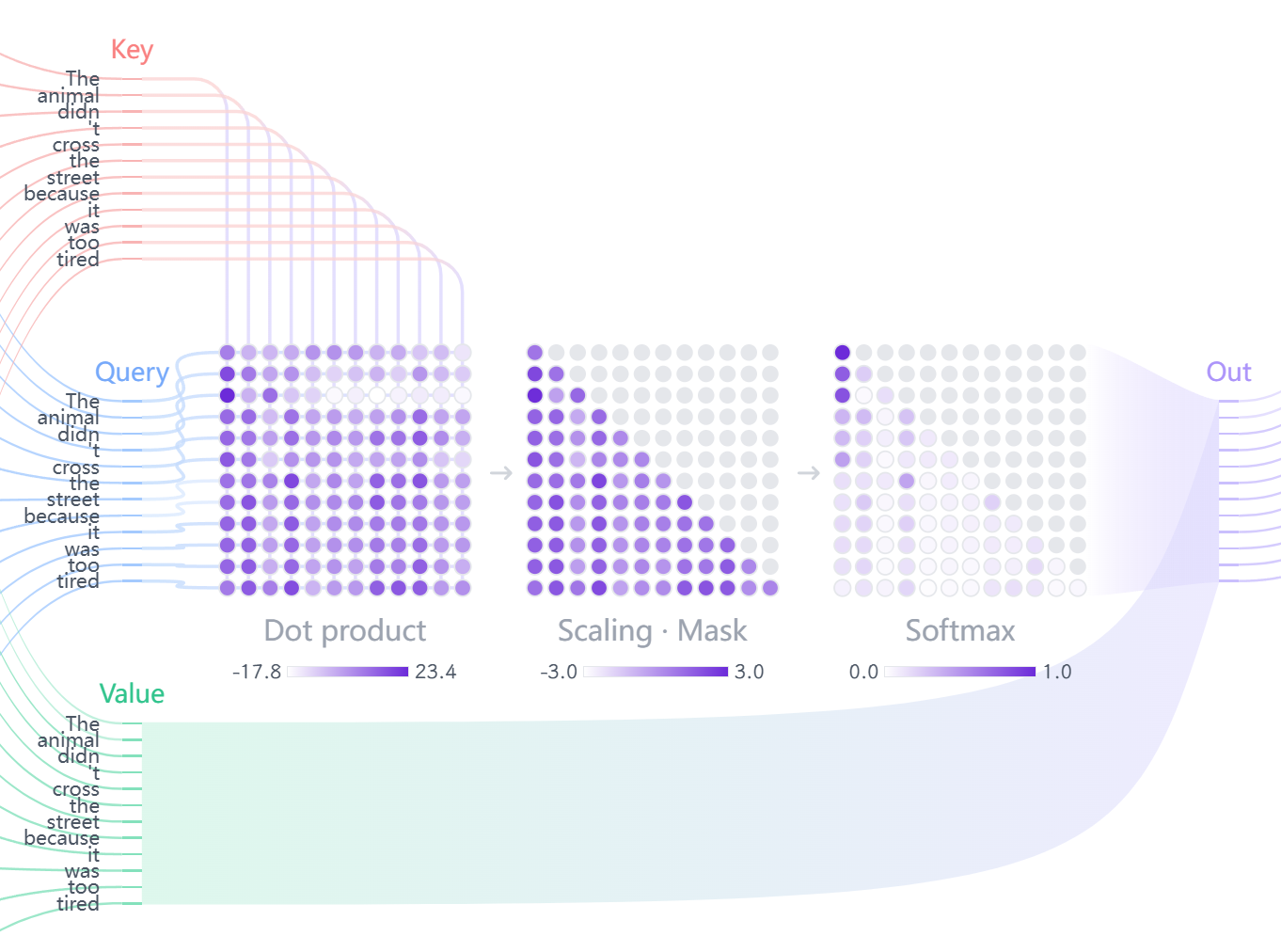
步骤 2:计算注意力分数
$$ S = QK^T \in \mathbb{R}^{n \times n} $$矩阵 $S$ 的第 $(i, j)$ 元素:
$$ S_{ij} = q_i \cdot k_j = \sum_{\ell=1}^{d_k} q_{i\ell} k_{j\ell} $$这个点积衡量了第 $i$ 个查询与第 $j$ 个键的相似度。
步骤 3:缩放
$$ S' = \frac{S}{\sqrt{d_k}} = \frac{QK^T}{\sqrt{d_k}} $$步骤 4:Softmax 归一化
对 $S’$ 的每一行应用 Softmax:
$$ A_{ij} = \frac{\exp(S'_{ij})}{\sum_{k=1}^n \exp(S'_{ik})} $$结果 $A \in \mathbb{R}^{n \times n}$ 称为注意力权重矩阵,满足:
- $A_{ij} \geq 0$ (非负性)
- $\sum_{j=1}^n A_{ij} = 1$ (每行和为 1,概率分布)
步骤 5:加权求和
$$ Z = AV \in \mathbb{R}^{n \times d_v} $$输出矩阵 $Z$ 的第 $i$ 行:
$$ z_i = \sum_{j=1}^n A_{ij} v_j $$即第 $i$ 个输出是所有值向量的加权平均,权重由注意力决定。
2. 先看Scale,为什么是 $\sqrt{d_k}$?—— 方差稳定性的严格推导
这绝对是论文中最精妙的数学细节之一。缩放因子 $\sqrt{d_k}$ 不是随便选的"魔法数字",而是有严格的统计学理由。
2.1 目标
保持点积 $q \cdot k$ 的方差为 1,以防止 Softmax 函数饱和。
2.2 问题
当 $q$ 和 $k$ 的维度 $d_k$ 变大时,它们的点积 $q \cdot k$ 的方差会发生什么?
2.3 推导
我们来分析点积。首先明确符号和维度:
- $S \in \mathbb{R}^{n \times n}$:注意力分数矩阵
- $S_{ij}$:第 $i$ 个查询向量 $q_i \in \mathbb{R}^{d_k}$ 与第 $j$ 个键向量 $k_j \in \mathbb{R}^{d_k}$ 的点积
- $q_i, k_j$:分别是 $Q$ 和 $K$ 矩阵的第 $i$ 行和第 $j$ 行
对于固定的 $(i, j)$,点积计算为:
$$ S_{ij} = q_i \cdot k_j = \sum_{\ell=1}^{d_k} q_{i\ell} k_{j\ell} $$其中 $\ell$ 是向量维度索引($\ell = 1, 2, \ldots, d_k$),$q_{i\ell}$ 表示 $q_i$ 的第 $\ell$ 个分量。
维度变化说明:
- $q_i \in \mathbb{R}^{d_k}$(行向量)
- $k_j \in \mathbb{R}^{d_k}$(行向量)
- $S_{ij} \in \mathbb{R}$(标量)
- 点积操作:$\mathbb{R}^{d_k} \times \mathbb{R}^{d_k} \to \mathbb{R}$
为了简化推导,我们固定 $(i, j)$,记 $s = S_{ij}$,$q = q_i$,$k = k_j$,则:
$$ s = q \cdot k = \sum_{\ell=1}^{d_k} q_\ell k_\ell $$前提假设 (Assumption)
为了进行分析,我们做出两个合理的统计假设(这也是论文作者的隐含假设,与 Xavier/Glorot 初始化一致):
- $q$ 和 $k$ 的每个分量 $q_\ell$ 和 $k_\ell$($\ell = 1, 2, \ldots, d_k$)都是独立同分布 (i.i.d.) 的。
- 它们是从一个均值 $\mathbb{E} = 0$,方差 $\text{Var} = 1$ 的分布中抽取的。
形式化:
$$ \begin{aligned} \mathbb{E}[q_\ell] &= 0, \quad \mathbb{E}[k_\ell] = 0 \\ \text{Var}(q_\ell) &= 1, \quad \text{Var}(k_\ell) = 1 \end{aligned} $$其中 $\ell = 1, 2, \ldots, d_k$。
第 1 步:计算 $s$ 的均值 $\mathbb{E}[s]$
$$ \mathbb{E}[s] = \mathbb{E}\left[ \sum_{\ell=1}^{d_k} q_\ell k_\ell \right] $$根据期望的线性性质:
$$ \mathbb{E}[s] = \sum_{\ell=1}^{d_k} \mathbb{E}[q_\ell k_\ell] $$因为 $q_\ell$ 和 $k_\ell$ 相互独立,所以:
$$ \mathbb{E}[q_\ell k_\ell] = \mathbb{E}[q_\ell] \cdot \mathbb{E}[k_\ell] $$代入假设:
$$ \mathbb{E}[s] = \sum_{\ell=1}^{d_k} (\mathbb{E}[q_\ell] \cdot \mathbb{E}[k_\ell]) = \sum_{\ell=1}^{d_k} (0 \cdot 0) = 0 $$结论 1:点积 $s$ 的均值(期望)为 0。✓
第 2 步:计算 $s$ 的方差 $\text{Var}(s)$
$$ \text{Var}(s) = \text{Var}\left( \sum_{\ell=1}^{d_k} q_\ell k_\ell \right) $$因为 $q_\ell k_\ell$ 与 $q_m k_m$ ($\ell \neq m$) 之间是相互独立的($q_\ell$ 和 $q_m$ 独立,$k_\ell$ 和 $k_m$ 独立),所以 “和的方差等于方差的和” :
$$ \text{Var}(s) = \sum_{\ell=1}^{d_k} \text{Var}(q_\ell k_\ell) $$说明:这是概率论中的关键性质。对于独立随机变量 $X_1, X_2, \ldots, X_n$:
$$\text{Var}(X_1 + X_2 + \cdots + X_n) = \text{Var}(X_1) + \text{Var}(X_2) + \cdots + \text{Var}(X_n)$$
现在,我们只需要计算 $\text{Var}(q_\ell k_\ell)$。
第 3 步:计算 $\text{Var}(q_\ell k_\ell)$
根据方差的定义:
$$ \text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 $$应用到 $q_\ell k_\ell$:
$$ \text{Var}(q_\ell k_\ell) = \mathbb{E}[(q_\ell k_\ell)^2] - (\mathbb{E}[q_\ell k_\ell])^2 $$从第 1 步我们知道 $\mathbb{E}[q_\ell k_\ell] = 0$,所以:
$$ \text{Var}(q_\ell k_\ell) = \mathbb{E}[(q_\ell k_\ell)^2] = \mathbb{E}[q_\ell^2 k_\ell^2] $$因为 $q_\ell$ 和 $k_\ell$ 独立,所以 $q_\ell^2$ 和 $k_\ell^2$ 也独立:
$$ \mathbb{E}[q_\ell^2 k_\ell^2] = \mathbb{E}[q_\ell^2] \cdot \mathbb{E}[k_\ell^2] $$第 4 步:计算 $\mathbb{E}[q_\ell^2]$
我们需要知道 $\mathbb{E}[q_\ell^2]$ 是什么。再次使用方差公式:
$$ \text{Var}(q_\ell) = \mathbb{E}[q_\ell^2] - (\mathbb{E}[q_\ell])^2 $$根据我们的假设:$\text{Var}(q_\ell) = 1$ 且 $\mathbb{E}[q_\ell] = 0$:
$$ 1 = \mathbb{E}[q_\ell^2] - (0)^2 \quad \Rightarrow \quad \mathbb{E}[q_\ell^2] = 1 $$同理,$\mathbb{E}[k_\ell^2] = 1$。
第 5 步:回代
将结果代入:
$$ \text{Var}(q_\ell k_\ell) = \mathbb{E}[q_\ell^2] \cdot \mathbb{E}[k_\ell^2] = 1 \cdot 1 = 1 $$最后,将它代入 $s$ 的方差总和中:
$$ \text{Var}(s) = \sum_{\ell=1}^{d_k} \text{Var}(q_\ell k_\ell) = \sum_{\ell=1}^{d_k} 1 = d_k $$2.4 关键结论
$$ \boxed{\text{Var}(q \cdot k) = d_k} $$点积的方差等于它的维度 $d_k$。
2.5 后果分析
这个结论意味着:
- 如果 $d_k = 64$:$\text{Var}(s) = 64$,标准差 $\sigma = \sqrt{64} = 8$
- 如果 $d_k = 512$:$\text{Var}(s) = 512$,标准差 $\sigma = \sqrt{512} \approx 22.6$
维度 $d_k$ 越大,点积 $s$ 的值就会(在 0 附近)波动得越剧烈。
根据"3-sigma 规则",大约 99.7% 的值会落在 $[\mu - 3\sigma, \mu + 3\sigma]$ 内。由于 $\mu = 0$:
- $d_k = 512$ 时:点积值约在 $[-68, 68]$ 范围内
2.6 对 Softmax 的影响
2.6.1 Softmax 函数的定义与性质
对于输入向量 $\mathbf{z} = [z_1, z_2, \ldots, z_n] \in \mathbb{R}^n$,Softmax 函数定义为:
$$ \text{softmax}(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{i=1}^n e^{z_i}} = \frac{e^{z_j}}{Z} $$其中 $Z = \sum_{i=1}^n e^{z_i}$ 是归一化常数(配分函数)。
关键性质:
- 非负性:$\text{softmax}(\mathbf{z})_j \geq 0$(因为指数函数 $e^{z_j} > 0$)
- 归一性:$\sum_{j=1}^n \text{softmax}(\mathbf{z})_j = 1$(概率分布)
- 单调性:如果 $z_i > z_j$,则 $\text{softmax}(\mathbf{z})_i > \text{softmax}(\mathbf{z})_j$
2.6.2 数值稳定性技巧
实际计算中,为了避免数值溢出,通常使用"减去最大值"的技巧:
$$ \text{softmax}(\mathbf{z})_j = \frac{e^{z_j - \max(\mathbf{z})}}{\sum_{i=1}^n e^{z_i - \max(\mathbf{z})}} $$其中 $\max(\mathbf{z}) = \max{z_1, z_2, \ldots, z_n}$。
为什么这样做?
- 指数函数增长极快:$e^{50} \approx 5.18 \times 10^{21}$,可能超出浮点数表示范围
- 减去最大值后,最大的指数项变为 $e^0 = 1$,其他项为负指数,数值稳定
- 数学上等价(分子分母同除以 $e^{\max(\mathbf{z})}$)
2.6.3 问题:Softmax 对极端输入敏感
问题:Softmax 对非常大或非常小的输入值非常敏感。
如果输入(即我们的点积 $s$)的方差很大(比如 512),就意味着很多 $s_j$ 的值会是 $+20, -15, +30$ 这样的极端值。
数值示例:
- $e^{20} \approx 4.85 \times 10^8$ 已经是一个天文数字
- $e^{-15} \approx 3.06 \times 10^{-7}$ 几乎为 0
具体例子:
考虑输入向量 $\mathbf{z} = [50, 1, 1, 1]$($n=4$):
$$ \begin{aligned} \text{softmax}([50, 1, 1, 1])_1 &= \frac{e^{50}}{e^{50} + e + e + e} = \frac{e^{50}}{e^{50} + 3e} \\ &\approx \frac{5.18 \times 10^{21}}{5.18 \times 10^{21} + 8.15} \\ &\approx \frac{5.18 \times 10^{21}}{5.18 \times 10^{21}} = 1.0 \end{aligned} $$对于 $j = 2, 3, 4$:
$$ \text{softmax}([50, 1, 1, 1])_j = \frac{e}{e^{50} + 3e} \approx \frac{2.72}{5.18 \times 10^{21}} \approx 0.0 $$因此:
$$ \text{softmax}([50, 1, 1, 1]) \approx [1.0, 0.0, 0.0, 0.0] $$这会导致 Softmax 的输出饱和 (saturate),变成一个接近"one-hot"的向量(例如 $[1, 0, 0, 0]$)。
2.7 梯度消失问题:Softmax 梯度的详细推导
当 Softmax 输出饱和时,梯度会消失 (Vanishing Gradients),因为 Softmax 的梯度在这些饱和区域几乎为 0。
2.7.1 Softmax 梯度的推导
设 $\mathbf{z} = [z_1, z_2, \ldots, z_n]$,\(p_j = \text{softmax}(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{i=1}^n e^{z_i}}\)。(这里涉及向量求导的雅可比矩阵计算,详情可以到矩阵微分笔记查看)
我们需要计算:
$$ \frac{\partial p_j}{\partial z_k} = \frac{\partial}{\partial z_k} \left( \frac{e^{z_j}}{\sum_{i=1}^n e^{z_i}} \right) $$情况 1:$j = k$(对角元素)
使用商的求导法则:
$$ \frac{\partial p_j}{\partial z_j} = \frac{e^{z_j} \cdot \sum_{i=1}^n e^{z_i} - e^{z_j} \cdot e^{z_j}}{(\sum_{i=1}^n e^{z_i})^2} $$化简:
$$ \begin{aligned} \frac{\partial p_j}{\partial z_j} &= \frac{e^{z_j}(\sum_{i=1}^n e^{z_i} - e^{z_j})}{(\sum_{i=1}^n e^{z_i})^2} \\ &= \frac{e^{z_j}}{\sum_{i=1}^n e^{z_i}} \cdot \frac{\sum_{i=1}^n e^{z_i} - e^{z_j}}{\sum_{i=1}^n e^{z_i}} \\ &= p_j \cdot (1 - p_j) \end{aligned} $$情况 2:$j \neq k$(非对角元素)
$$ \frac{\partial p_j}{\partial z_k} = \frac{0 \cdot \sum_{i=1}^n e^{z_i} - e^{z_j} \cdot e^{z_k}}{(\sum_{i=1}^n e^{z_i})^2} = -\frac{e^{z_j} e^{z_k}}{(\sum_{i=1}^n e^{z_i})^2} $$化简:
$$ \begin{aligned} \frac{\partial p_j}{\partial z_k} &= -\frac{e^{z_j}}{\sum_{i=1}^n e^{z_i}} \cdot \frac{e^{z_k}}{\sum_{i=1}^n e^{z_i}} \\ &= -p_j \cdot p_k \end{aligned} $$2.7.2 统一公式
使用 Kronecker delta $\delta_{jk}$($j=k$ 时为 1,否则为 0),可以统一两种情况:
$$ \frac{\partial p_j}{\partial z_k} = p_j (\delta_{jk} - p_k) $$验证:
- 当 $j = k$:$\frac{\partial p_j}{\partial z_j} = p_j (1 - p_j)$ ✓
- 当 $j \neq k$:$\frac{\partial p_j}{\partial z_k} = p_j (0 - p_k) = -p_j p_k$ ✓
2.7.3 梯度消失的数值分析
使用之前的例子:$\mathbf{z} = [50, 1, 1, 1]$,则 $\mathbf{p} = \text{softmax}(\mathbf{z}) \approx [1.0, 0.0, 0.0, 0.0]$。
计算梯度矩阵 $\frac{\partial p_j}{\partial z_k}$:
对于 $j = 1$(第一个元素):
$$ \begin{aligned} \frac{\partial p_1}{\partial z_1} &= p_1 (1 - p_1) = 1.0 \cdot (1 - 1.0) = 0 \\ \frac{\partial p_1}{\partial z_2} &= p_1 (0 - p_2) = 1.0 \cdot (0 - 0) = 0 \\ \frac{\partial p_1}{\partial z_3} &= p_1 (0 - p_3) = 1.0 \cdot (0 - 0) = 0 \\ \frac{\partial p_1}{\partial z_4} &= p_1 (0 - p_4) = 1.0 \cdot (0 - 0) = 0 \end{aligned} $$对于 $j = 2, 3, 4$:
$$ \frac{\partial p_j}{\partial z_k} = p_j (\delta_{jk} - p_k) \approx 0 \cdot (\delta_{jk} - \cdot) = 0 $$结论:梯度矩阵几乎全为 0!
2.7.4 梯度消失的后果
当 $\text{softmax}(z_i) \approx 0$ 或 $\approx 1$ 时:
- 如果 $p_i \approx 0$:梯度 $\frac{\partial p_i}{\partial z_k} = p_i (\delta_{ik} - p_k) \approx 0 \cdot (\cdot) \approx 0$
- 如果 $p_i \approx 1$:
- 对于 $k = i$:$\frac{\partial p_i}{\partial z_i} = p_i (1 - p_i) \approx 1 \cdot (1 - 1) = 0$
- 对于 $k \neq i$:$\frac{\partial p_i}{\partial z_k} = p_i (0 - p_k) \approx 1 \cdot (0 - 0) = 0$
结果:模型将停止学习,因为梯度无法反向传播,参数无法更新。
2.8 解决方案:缩放
我们希望将 $s$ 的方差"拉回"到 1。
关键性质:方差的缩放性质
对于随机变量 $X$ 和常数 $c$:
$$ \text{Var}(c \cdot X) = c^2 \cdot \text{Var}(X) $$证明:
$$ > \begin{align} > \text{Var}(cX) &= \mathbb{E}[(cX - \mathbb{E}[cX])^2] \phantom{= c^2 \mathbb{E}[(X - \mathbb{E}[X])^2]} \\ > &= \mathbb{E}[(cX - c\mathbb{E}[X])^2] \phantom{= c^2 \text{Var}(X)} \\ > &= c^2 \mathbb{E}[(X - \mathbb{E}[X])^2] \\ > &= c^2 \text{Var}(X) > \end{align} > $$
求解常数 $c$
我们希望找到一个常数 $c$,使得:
$$ \text{Var}(c \cdot s) = 1 $$应用性质:
$$ c^2 \cdot \text{Var}(s) = 1 $$代入 $\text{Var}(s) = d_k$:
$$ c^2 \cdot d_k = 1 $$解得:
$$ c^2 = \frac{1}{d_k} \quad \Rightarrow \quad c = \frac{1}{\sqrt{d_k}} $$2.9 最终推论
我们不应该使用原始点积 $s$,而应该使用缩放后的点积:
$$ s' = c \cdot s = \frac{s}{\sqrt{d_k}} = \frac{q \cdot k}{\sqrt{d_k}} $$这个新的缩放后的分数 $s’$ 的方差是:
$$ \text{Var}(s') = \text{Var}\left(\frac{s}{\sqrt{d_k}}\right) = \left(\frac{1}{\sqrt{d_k}}\right)^2 \cdot \text{Var}(s) = \frac{1}{d_k} \cdot d_k = 1 $$$$ \boxed{\text{Var}\left(\frac{q \cdot k}{\sqrt{d_k}}\right) = 1} $$2.10 总结
通过除以 $\sqrt{d_k}$,我们将点积得分的方差从 $d_k$ 重新标准化回 1,使其独立于维度 $d_k$ 的大小。
这保证了:
- Softmax 的输入始终处于一个"合理"的、非饱和的范围(通常在 $[-3, 3]$ 内)
- 梯度能够稳定流动
- 模型得以成功训练
这就是 “Scaled” Dot-Product Attention 中 “Scaled” 的精确数学含义。
3. 再看Dot-Product,注意力设计的核心决策
选择点积作为 Query 和 Key 之间的相似度(Score)计算方式,是 Transformer 区别于以往注意力机制的核心设计决策之一,这个决策的出发点是极致的计算效率。
1. 问题的提出:如何衡量 Q 和 K 的“相关性”?
自注意力的核心是 $q_i$(查询)需要评估它与所有 $k_j$(键)的相关性。我们需要一个函数 $f(\text{Score})$ 来计算这个相关性:
$$ \text{Score}_{ij} = f(q_i, k_j) $$在 Transformer 之前,最主流的注意力机制(由 Bahdanau 在 2015 年提出,用于 RNN 翻译模型)使用的是 “加性注意力” (Additive Attention) ,也称为“拼接-tanh”注意力。
加性注意力的公式:
$$ f(q_i, k_j) = \mathbf{v}_a^T \cdot \tanh(W_a q_i + U_a k_j) $$- $W_a$ 和 $U_a$ 是两个可学习的权重矩阵。
- $\mathbf{v}_a$ 是一个可学习的权重向量。
- 它将 $q_i$ 和 $k_j$ 分别进行线性变换,然后相加,通过 $\tanh$ 非线性激活,最后再通过一个向量 $\mathbf{v}_a$ 投影为一个标量(分数)。
2. Transformer 的选择:点积注意力 (Dot-Product Attention)
“Attention Is All You Need” 论文的作者们抛弃了复杂的加性注意力,转而选择了数学上更简洁的点积:
$$ f(q_i, k_j) = q_i \cdot k_j $$这个选择的背后,是基于对计算效率和硬件(GPU)特性的深刻洞察。
为什么点积是关键?
2.1 核心优势:可矩阵化 (Matrix-friendly)
这是最重要的理由。
点积的本质:$q_i \cdot k_j$ 是向量 $q_i$(行向量)和 $k_j$(列向量,即 $k_j^T$)的乘法。
扩展到全局:当我们要计算所有 $q_i$ 对 所有 $k_j$ 的得分时,我们就得到了一个 $(N \times N)$ 的分数矩阵 $S$。
$$ S = \begin{bmatrix} q_1 \cdot k_1 & q_1 \cdot k_2 & \cdots & q_1 \cdot k_N \\ q_2 \cdot k_1 & q_2 \cdot k_2 & \cdots & q_2 \cdot k_N \\ \vdots & \vdots & \ddots & \vdots \\ q_N \cdot k_1 & q_N \cdot k_2 & \cdots & q_N \cdot k_N \end{bmatrix} $$数学等价:这个 $S$ 矩阵,在数学上严格等于 $Q$ 矩阵和 $K$ 矩阵转置的乘积:
$$S = Q K^T$$- $Q \in \mathbb{R}^{N \times d_k}$
- $K \in \mathbb{R}^{N \times d_k} \implies K^T \in \mathbb{R}^{d_k \times N}$
- $S \in \mathbb{R}^{N \times N}$
这个等价性是 Transformer 并行化的基石。
2.2 硬件亲和性 (Hardware-friendly)
- 加性注意力的计算:$f(q_i, k_j) = \mathbf{v}_a^T \cdot \tanh(W_a q_i + U_a k_j)$
- 要计算 $N \times N$ 的分数矩阵,这个计算必须(或者说很难避免)对 $N \times N$ 个 $(q_i, k_j)$ 对分别执行 $W_a q_i$, $U_a k_j$, $\tanh$, $\mathbf{v}_a^T$ 这一系列多步操作。加法注意力的 $\tanh$ 是逐元素操作,并行度受限这,在计算上是零碎的、低效的。
- 点积注意力的计算:$S = Q K^T$
- 这只是一个单一的、大规模的矩阵乘法 (GEMM - General Matrix Multiply)。
- BLAS 库(cuBLAS、MKL)对 GEMM(通用矩阵乘法)极度优化,现代 GPU 和 TPU(张量处理单元)就是为了执行这种大规模 GEMM 操作而专门优化设计的。
- 硬件可以在极高的并行度下,一次性完成 $Q K^T$ 这个操作,速度比执行 $N^2$ 次零碎的“加性”操作快几个数量级。
复杂度分析
点积注意力(Scaled Dot-Product Attention)
步骤 1:计算 $QK^T$
- 矩阵乘法:$(n \times d_k) \times (d_k \times n) = (n \times n)$
- 复杂度:$O(n^2 d_k)$
步骤 2:Softmax
- 对 $n \times n$ 矩阵的每一行归一化
- 复杂度:$O(n^2)$
步骤 3:计算 $AV$
- 矩阵乘法:$(n \times n) \times (n \times d_v) = (n \times d_v)$
- 复杂度:$O(n^2 d_v)$
总复杂度:
$$ > O(n^2 d_k) + O(n^2) + O(n^2 d_v) = O(n^2 d) > $$其中 $d = \max(d_k, d_v)$(通常 $d_k = d_v = d_{\text{model}}/h$,$h$ 是头数)。
加法注意力(Bahdanau Attention)
公式:
$$ > \text{score}(q, k) = v^T \tanh(W_1 q + W_2 k) > $$其中 $W_1, W_2 \in \mathbb{R}^{d_{\text{hidden}} \times d}$,$v \in \mathbb{R}^{d_{\text{hidden}}}$。
计算每个词对 $(i, j)$ 的分数:
- 计算 $W_1 q_i$:$O(d^2)$
- 计算 $W_2 k_j$:$O(d^2)$
- 加法和 $\tanh$:$O(d)$
- 计算 $v^T \cdot$:$O(d)$
每个词对:$O(d^2)$
总共 $n^2$ 个词对:
$$ > O(n^2 d^2) > $$对比
方法 时间复杂度 空间复杂度 点积注意力 $O(n^2 d)$ $O(n^2 + nd)$ 加法注意力 $O(n^2 d^2)$ $O(n^2 + nd)$ 结论:点积注意力少一个 $d$ 因子,更快。
2.3 简洁性与无参数
- 点积(在 Q/K 投影之后)是一个无参数 (non-parametric) 的相似度函数。它不引入像 $W_a, U_a, \mathbf{v}_a$ 这样的额外参数。
- 这使得模型结构更简洁,减少了参数量。
4. Q K V分离,attention的核心
4.1 核心问题一(QK的对称性破缺)
$W^Q$ 和 $W^K$ 在初始化时完全对称(同分布),且维度相同(都是 $\mathbb{R}^{d_{\text{model}} \times d_k}$)。那么:
- 为什么约定计算 $QK^T$ 而不是 $KQ^T$?
- Q 和 K 能否互换?
- 训练后它们为什么会分化?
1. 数学形式化
定义标准自注意力:
$$ A_{\text{std}} = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) $$如果交换 Q 和 K:
$$ A_{\text{swap}} = \text{softmax}\left(\frac{KQ^T}{\sqrt{d_k}}\right) $$2. 初始化阶段:统计等价性
假设采用 Xavier/Glorot 初始化:
$$ W^Q \sim \mathcal{N}\left(0, \frac{2}{d_{\text{model}} + d_k}\right), \quad W^K \sim \mathcal{N}\left(0, \frac{2}{d_{\text{model}} + d_k}\right) $$两者从相同分布独立采样,统计特性完全相同:
$$ \mathbb{E}[W^Q] = \mathbb{E}[W^K] = 0, \quad \text{Var}(W^Q) = \text{Var}(W^K) $$生成的 Q 和 K:
$$ Q = XW^Q, \quad K = XW^K $$考虑注意力分数矩阵:
$$ QK^T = XW^Q(W^K)^TX^T $$$$ KQ^T = XW^K(W^Q)^TX^T $$3. 对称性破缺的根源
根源一:矩阵惩罚的“不对称”
虽然 $W^Q(W^K)^T$ 和 $W^K(W^Q)^T$ 统计等价(同分布),但它们是不同的随机矩阵实例。
期望层面:
$$ \mathbb{E}[W^Q(W^K)^T] = \mathbb{E}[W^Q]\mathbb{E}[(W^K)^T] = 0 \cdot 0 = 0 $$(零均值矩阵)
但实际实例不同:
$$ W^Q(W^K)^T \neq W^K(W^Q)^T $$原因:矩阵乘法不满足交换律($AB \neq BA$ 一般情况下)。但其实对于完全随机初始化的矩阵来说,我依然认为二者在数学意义上是等价的,但这种差异会在反向传播时被体现出来。
根源二:Softmax 的行归一化 (Row-wise Normalization)(关键)
这是更根本的、结构性的不对称。
标准的注意力矩阵 $A$ 定义为 $S = QK^T$ 按行 $\text{softmax}$:
$$ A_{ij} = \text{softmax}(S_i)_j = \frac{\exp(S_{ij})}{\sum_{k=1}^N \exp(S_{ik})} = \frac{\exp(q_i \cdot k_j)}{\sum_{k=1}^N \exp(q_i \cdot k_k)} $$- 物理含义:$A_{ij}$ 表示 Query $i$(第 $i$ 行)将其 100% 的注意力 “分配” 给 Key $j$ (第 $j$ 列)的权重。
- 归一化维度:分母 $\sum_{k=1}^N \dots$ 是对所有 Key(即 $k=1 \dots N$)求和。
如果我们交换 Q 和 K,我们得到 $A_{\text{swap}} = \text{softmax}(KQ^T) = \text{softmax}(S^T)$:
$$ (A_{\text{swap}})_{ij} = \text{softmax}((S^T)_i)_j = \frac{\exp((S^T)_{ij})}{\sum_{k=1}^N \exp((S^T)_{ik})} = \frac{\exp(S_{ji})}{\sum_{k=1}^N \exp(S_{ki})} $$$$ (A_{\text{swap}})_{ij} = \frac{\exp(q_j \cdot k_i)}{\sum_{k=1}^N \exp(q_k \cdot k_i)} $$- 物理含义:$(A_{\text{swap}})_{ij}$ 表示 Key $i$(第 $i$ 行)从 Query $j$(第 $j$ 列)处 “接收” 到的注意力,占其从所有 Query (即 $k=1 \dots N$)接收到的总和的比例。
- 归一化维度:分母 $\sum_{k=1}^N \dots$ 是对所有 Query(即 $k=1 \dots N$)求和。
结论:$A$ 和 $A_{\text{swap}}$ 的分母(归一化项)完全不同,它们在数学上和语义上回答的是两个不同的问题。
$$ A_{ij} \text{ (Query } i \text{ 的输出分布)} \neq (A_{\text{swap}})_{ji} \text{ (Query } i \text{ 的输入分布)} $$$\text{softmax}$ 的行归一化操作,从结构上决定了 $Q$ (行) 和 $K$ (列) 的角色不可互换。
根源三:反向传播梯度的不对称
前向传播的结构不对称,必然导致反向传播的梯度路径不对称。
反向传播时,损失函数 $\mathcal{L}$ 对 $W^Q$ 和 $W^K$ 的梯度不同:
$$ \frac{\partial \mathcal{L}}{\partial W^Q} = \frac{\partial \mathcal{L}}{\partial Q} \frac{\partial Q}{\partial W^Q} = \frac{\partial \mathcal{L}}{\partial Q} \cdot X^T $$$$ \frac{\partial \mathcal{L}}{\partial W^K} = \frac{\partial \mathcal{L}}{\partial K} \frac{\partial K}{\partial W^K} = \frac{\partial \mathcal{L}}{\partial K} \cdot X^T $$这里$\frac{\partial \mathcal{L}}{\partial W^Q}$和$\frac{\partial \mathcal{L}}{\partial W^Q}$的求导参考笔记的标量对矩阵求导内容,也是全连接层的求导形式。
关键问题:$\frac{\partial \mathcal{L}}{\partial Q}$ 和 $\frac{\partial \mathcal{L}}{\partial K}$ 相等吗?
答案:不相等
考虑注意力机制的前向传播:
$$ S = QK^T, \quad A = \text{softmax}(S), \quad \text{Out} = AV $$对于 $S = QK^T$ 的梯度(链式法则):
$$ \frac{\partial S}{\partial Q} = K, \quad \frac{\partial S}{\partial K} = Q $$更详细地,假设上游梯度为 $\frac{\partial \mathcal{L}}{\partial S} \in \mathbb{R}^{n \times n}$:
$$ \frac{\partial \mathcal{L}}{\partial Q} = \frac{\partial \mathcal{L}}{\partial S} \cdot \frac{\partial S}{\partial Q} = \frac{\partial \mathcal{L}}{\partial S} \cdot K $$$$ \frac{\partial \mathcal{L}}{\partial K} = \frac{\partial \mathcal{L}}{\partial S} \cdot \frac{\partial S}{\partial K}^T = \left(\frac{\partial \mathcal{L}}{\partial S}\right)^T \cdot Q $$推导细节:对于 $S_{ij} = \sum_\ell Q_{i\ell} K_{j\ell}$:
$$\frac{\partial S_{ij}}{\partial Q_{i\ell}} = K_{j\ell}, \quad \frac{\partial S_{ij}}{\partial K_{j\ell}} = Q_{i\ell}$$
结论:
$$ \frac{\partial \mathcal{L}}{\partial Q} = \frac{\partial \mathcal{L}}{\partial S} \cdot K $$$$ \frac{\partial \mathcal{L}}{\partial K} = \left(\frac{\partial \mathcal{L}}{\partial S}\right)^T \cdot Q $$两者结构完全不同!
- $\frac{\partial \mathcal{L}}{\partial Q}$ 是 $\frac{\partial \mathcal{L}}{\partial S}$ 右乘 $K$
- $\frac{\partial \mathcal{L}}{\partial K}$ 是 $\frac{\partial \mathcal{L}}{\partial S}$ 的转置右乘 $Q$
4. 对称性破缺的放大
参数更新:
$$ W^Q \leftarrow W^Q - \eta \frac{\partial \mathcal{L}}{\partial W^Q} $$$$ W^K \leftarrow W^K - \eta \frac{\partial \mathcal{L}}{\partial W^K} $$训练过程是一个正反馈循环:
- $t=0$:$W^Q_0$ 和 $W^K_0$ 存在微小的实例不对称。
- 前向传播:$\text{softmax}$ 的结构不对称利用了 $W^Q_0 \neq W^K_0$。
- 反向传播:产生不对称的梯度 $\frac{\partial \mathcal{L}}{\partial W^Q_0} \neq \frac{\partial \mathcal{L}}{\partial W^K_0}$。
- 参数更新:$W^Q_1$ 和 $W^K_1$ 被推向不同的方向。
- $t=1$:$|W^Q_1 - W^K_1|$ 的差异被放大,导致下一步的梯度差异更大。
4.2 核心问题二(KV的功能解耦)
K/V 分离(Key 和 Value 的分离)是自注意力机制的一个关键设计,它将 “匹配/决策” 过程与 “信息/内容” 过程进行了解耦 (Decoupling)
我们可以通过一个“反事实推导”来理解它的必要性:假如 K 和 V 不分离(即 K=V),模型会遇到什么问题?
1. 假设情景:K=V 不分离
如果 K 和 V 不分离,这意味着我们只使用一个投影矩阵 $W^{KV}$ 来同时生成 Key 和 Value 向量。
输入: $X \in \mathbb{R}^{N \times d_{\text{model}}}$
投影:
- $Q = X W^Q$
- $K = X W^{KV}$
- $V = X W^{KV}$
因此:$K = V$
注意力公式将变为:
$$ Z = \text{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) K $$
在这个公式中,同一个向量 $k_j$($K$ 矩阵的第 $j$ 行)被迫扮演两个截然不同的角色。
2. 理论推导:“功能冲突” (Functional Conflict)
在 $K=V$ 的设定下, $W^{KV}$ 矩阵在反向传播中会收到来自两条不同路径的梯度,而这两条路径的优化目标是相互冲突的。
我们来看 $Z_i$(输出的第 $i$ 行)的计算:
$$ Z_i = \sum_{j=1}^N A_{ij} \cdot v_j = \sum_{j=1}^N A_{ij} \cdot k_j $$其中 $A_{ij} = \text{softmax}(q_i \cdot k_j / \sqrt{d_k})$
$W^{KV}$ 矩阵的参数会通过 $k_j$ 影响最终的损失 $\mathcal{L}$。根据链式法则,$\mathcal{L}$ 对 $W^{KV}$ 的梯度 $\frac{\partial \mathcal{L}}{\partial W^{KV}}$ 至少来自两个源头:
- 路径一:作为 K (Key) 的梯度,用于“决策”
- $k_j$ 出现在 $\text{softmax}$ 内部,作为 $q_i \cdot k_j$ 的一部分。
- $W^{KV}$ 的梯度会包含 $\frac{\partial \mathcal{L}}{\partial A_{ij}} \frac{\partial A_{ij}}{\partial k_j}$ 这一项。
- 优化目标:这条路径的梯度会迫使 $W^{KV}$ 去调整 $k_j$ 向量,使其成为一个 “优秀的索引 (Key)” 。
- “优秀”的定义:$k_j$ 的向量方向应该能与相关的 $q_i$(查询)产生高点积,与不相关的 $q_l$ 产生低点积。这个向量的“使命”是 “被匹配” 。
- 路径二:作为 V (Value) 的梯度,用于“内容”
- $k_j$ 出现在 $\text{softmax}$ 外部,作为被加权求和的对象 $A_{ij} \cdot k_j$。
- $W^{KV}$ 的梯度会包含 $\frac{\partial \mathcal{L}}{\partial Z_i} \frac{\partial Z_i}{\partial k_j}$ 这一项,即 $\frac{\partial \mathcal{L}}{\partial Z_i} \cdot A_{ij}$。
- 优化目标:这条路径的梯度会迫使 $W^{KV}$ 去调整 $k_j$ 向量,使其成为一个 “优秀的内容 (Value)” 。
- “优秀”的定义:$k_j$ 必须包含 $x_j$ 原始的、丰富的语义信息,以便当它被 $A_{ij}$ 选中并加权求和后,能为 $Z_i$(下一层的输入)提供有价值的信息。这个向量的“使命”是 “被聚合” 。
3. 冲突点(The Conflict)
一个向量空间,无法同时最优地服务于两个目标。
- 为了成为一个好的 Key, $k_j$ 向量空间可能会演化成一个“关系空间”,其中向量的“方向”比“内容”更重要。例如,模型可能会发现,所有“代词”的 $q$ 和所有“名词”的 $k$ 在某个子空间上对齐会很有利。
- 为了成为一个好的 Value, $k_j$ 向量空间必须是一个“语义空间”,它需要保留 $x_j$ 的原始含义(比如“animal”和“street”的语义必须有明确区分)。
如果 $K=V$, $W^{KV}$ 矩阵被迫在“优化匹配关系”和“保留语义内容”之间找到一个糟糕的妥协 (Suboptimal Compromise)。这在优化上是一个表征瓶颈 (Representational Bottleneck)。
4.3 语义角色的涌现
- 无论是这种由随机初始化触发、被非对称结构定义、由梯度更新放大的对称性破缺,迫使 $W^Q$ 和 $W^K$ 必须“分道扬镳”以最小化损失。
- 还是$K$,$V$在责任分配上的解耦,$W^K$ 专精于“匹配”,$W^V$ 专精于“内容”,消除了 $K=V$ 时的表征瓶颈
总结,这种“分工”是SDPA设计哲学与数据驱动的涌现行为:
- $W^Q$ (Query 投影):被训练来将 $X$ 投影到一 个“查询/提问”空间。它学会了为 $x_i$ 生成一个向量 $q_i$,其“意图”是 “我需要什么信息?”
- 例:$q_{\text{it}}$ (来自"it") $\rightarrow$ “我需要一个指代对象。”
- $W^K$ (Key 投影):被训练来将 $X$ 投影到一个“键/索引”空间。它学会了为 $x_j$ 生成一个向量 $k_j$,其“意图”是 “我能提供什么信息?”
- 例:$k_{\text{animal}}$ (来自"animal") $\rightarrow$ “我是一个潜在的指代对象。”
- $W^V$ (Value投影):被训练来将 $X$ 投影到一个“键/索引”空间。它学会了为 $x_j$ 生成一个向量 $v_j$,其“意图”是 “我代表什么语义内容?”
- 例:$v_{\text{animal}}$ (来自"animal") $\rightarrow$ “我是这个指代对象本身蕴含着怎样的属性、语义。”
5. 小结:SDPA 的三个支柱
Scaled Dot-Product Attention 的设计建立在三个核心支柱上:
| 设计选择 | 数学依据 | 效果 |
|---|---|---|
| 缩放因子 $\sqrt{d_k}$ | $\text{Var}(\frac{s}{\sqrt{d_k}}) = 1$ 防止 Softmax 饱和 | 方差稳定、梯度健康、训练收敛 |
| 点积相似度 | 复杂度 $O(n^2 d)$ vs $O(n^2 d^2)$ 矩阵乘法硬件优化 | 计算高效、硬件友好 |
| Q-K-V 分离 | 梯度不对称:$\frac{\partial \mathcal{L}}{\partial Q} \neq \frac{\partial \mathcal{L}}{\partial K}$ 对称性破缺 | 有向关系建模、表达力强、语义角色分化 |
理论设计与工程实践的统一
SDPA 的设计体现了深度学习的一个核心哲学:
优雅的数学往往带来高效的工程实现。
- 理论保证(方差稳定性)→ 训练稳定
- 简单形式(点积)→ 计算高效
- 对称破缺(Q-K 分化)→ 表达能力
这三个支柱共同支撑起 Transformer 的强大性能,使其成为现代 AI 的基石。
参考与延伸阅读
- 原始论文:Vaswani et al., “Attention is All You Need”, NeurIPS 2017
- 初始化理论:Glorot & Bengio, “Understanding the difficulty of training deep feedforward neural networks”, AISTATS 2010
- 复杂度分析:Tay et al., “Efficient Transformers: A Survey”, ACM Computing Surveys 2022
以上内容参考了多个博客帖子以及我向Gemini老师问道后的总结整理,仅经过我个人的推导和求证,请辩证的看待。如有问题,欢迎在下放评论区留言或者邮件交流学习!