摘要
本笔记基于论文 “Attention is All You Need” (Vaswani et al., 2017),结合 Transformer Explainer 可视化工具和相关博客资料,系统梳理 Transformer 架构的核心思想。
Transformer 是一个具有里程碑意义的神经网络架构,它从根本上改变了人工智能的发展方向。自 2017 年提出以来,Transformer 已成为深度学习的主流架构,支撑着 OpenAI 的 GPT、Meta 的 Llama、Google 的 Gemini 等文本生成模型。不仅如此,Transformer 还被应用于音频生成、图像识别、蛋白质结构预测,甚至游戏对弈等众多领域,展现了其跨域的强大能力。
1. 引言
1.1 Transformer 出现前的时代:RNN 和 LSTM
在 Transformer 出现之前,处理序列数据(如句子、语音或时间序列)的主流模型是循环神经网络(Recurrent Neural Networks, RNN) ,特别是其高级变体:LSTM(Long Short-Term Memory,长短期记忆) 和 GRU(Gated Recurrent Unit,门控循环单元) 。
RNN 的核心思想
RNN 的设计理念非常直观:它像人类阅读一样,逐个处理序列中的元素(例如,一个一个地读取单词)。
假设我们要处理句子 “I am a student”:
- 第 1 步:RNN 读取第一个单词 “I”,生成一个"记忆"或"摘要",称为隐藏状态(hidden state)记作
h_I - 第 2 步:RNN 读取第二个单词 “am”,结合当前单词信息和上一步的隐藏状态
h_I,生成新的隐藏状态h_am - 第 3 步:读取 “a”,结合
h_am,生成h_a - 第 4 步:读取 “student”,结合
h_a,生成h_student
最终的隐藏状态(或每一步状态的组合)就被认为是整个句子的编码表示。
这种递归结构在理论上非常适合处理序列,因为它自然地捕捉了单词的顺序和上下文关系。
1.2 RNN/LSTM 的两大瓶颈
然而,RNN 的这种"循环"或"串行"特性也正是其最大的问题所在。
问题 1:信息传递的瓶颈——长程依赖难题
在 RNN 中,信息必须逐步传递。如果一个句子有 50 个单词:
- 第 1 个单词的信息要传递到第 50 个单词,必须"走过" 49 步
- 每一步传递都会有信息的损耗或变形
- 这导致了著名的梯度消失/梯度爆炸问题
用一个形象的比喻:RNN 就像电话游戏(传话游戏) 。
- 第一个人说:“今天天气真好”
- 传到第二个人:“今天天气好”
- 传到第三个人:“今天很好”
- …
- 传到第 10 个人:“好”
信息在逐步传递的过程中逐渐失真,远处的重要信息很难完整保留。
虽然 LSTM 通过引入"门控机制"(Gate Mechanism)缓解了这个问题,但并未从根本上解决。
问题 2:计算效率的瓶颈——无法并行化
RNN 的计算是绝对串行的:
h_I → h_am → h_a → h_student
- 你必须先计算完
h_I,才能计算h_am - 你无法在计算
h_I的同时,去计算h_a - 每一步的计算都依赖于前一步的结果
这在现代硬件(如 GPU)上是个致命缺陷:
- GPU 的优势在于大规模并行计算(同时计算成千上万个矩阵元素)
- 但 RNN 的串行特性让 GPU 大部分算力都在"等待"
- 训练速度极慢,尤其在处理长序列或大规模数据集时
1.3 核心矛盾的总结
| 特性 | RNN/LSTM 的局限 |
|---|---|
| 信息路径 | 远距离单词间的信息需要逐步传递,容易失真(梯度消失) |
| 计算方式 | 串行计算,必须等待前一步完成 |
| 硬件利用 | 无法充分利用 GPU 的并行计算能力 |
| 训练效率 | 在大规模数据集上训练极慢 |
2. Transformer 的核心创新:自注意力机制
2.1 革命性的转变
Transformer 的核心突破在于:完全抛弃了循环结构,转而使用自注意力机制(Self-Attention Mechanism) 。
关键创新 1:并行化计算
还是用句子 “I am a student” 为例。
在 Transformer 的 编码器(Encoder)中:
- 计算 “student” 的表示时,模型可以一步到位地、直接看到 “I”, “am”, “a” 三个词
- 计算 “am” 的表示时,也同时看到 “I”, “a”, “student”
- 所有单词的计算是同时进行的
这不是通过 h_am 间接"传递"信息给 h_a,而是像一个全连接图,所有单词在同一时间互相"观察"(计算注意力分数)。
这个"观察"的过程,在数学上是一个大规模的矩阵乘法。而 GPU 极其擅长并行计算矩阵乘法!无论句子是 10 个词还是 50 个词,计算所有词的表示都只需要一次矩阵运算的时间。
关键创新 2:直接的长程依赖
在 Transformer 中:
- 第 1 个单词到第 50 个单词的信息传递:一步直达
- 没有逐步传递造成的信息损耗
- 模型可以直接捕捉任意距离的依赖关系
用比喻来说:Transformer 就像一个圆桌会议。
- 所有人(所有单词)同时在场
- 主持人(当前单词)可以直接询问(Query)在场的每一个人(Key)
- 所有人(Value)同时把信息汇总给主持人
- 没有中间的传话环节
2.2 训练 vs 推理:并行与串行的平衡
这里需要澄清一个重要的概念混淆:
在训练(Training)时:完全并行
在训练 Transformer 时(以翻译任务为例:“I am a student” → “我 是 一名 学生”):
- 我们会把正确答案 “我 是 一名 学生” 整个喂给解码器(Decoder)
- 所有位置(“我”, “是”, “一名”, “学生”)的计算在一个大矩阵中并行完成
- 为了防止"作弊"(即防止 “一名” 偷看到未来的 “学生”),使用带掩码的自注意力(Masked Self-Attention) :
- 计算 “我” 时,只能看到 “我”
- 计算 “是” 时,能看到 “我” 和 “是”
- 计算 “一名” 时,能看到 “我”, “是”, “一名”
- 掩码通过将"未来"词的注意力分数设为负无穷实现
关键:虽然有掩码,但计算本身是并行的!
在推理(Inference)时:自回归串行
在生成文本时(如 GPT 生成回答):
- 必须先生成第 1 个词,才能生成第 2 个词
- 这是自回归(Auto-regressive)的特性
- 这部分确实是串行的
但即使在推理时,Transformer 相比 RNN 仍有优势:
- 编码器部分(理解输入)仍然是并行的
- 每一步生成都能直接访问所有历史信息,无需逐步传递
2.3 小结
Transformer 通过自注意力机制实现了两个革命性突破:
- 并行化:充分利用现代硬件(GPU/TPU)的并行计算能力,训练速度大幅提升
- 长程依赖:任意距离的单词间可以直接交互,无需逐步传递信息
这使得 Transformer 能够在超大规模数据集(如整个互联网的文本)上训练,成为现代大语言模型(如 GPT、BERT、Llama)的基础架构。
正如论文标题所言:"Attention is All You Need"(注意力就是你所需要的一切)。
3. 自注意力机制的数学原理
前面我们从宏观角度理解了自注意力的优势,现在让我们深入其内部,看看它到底是如何工作的。
3.1 核心思想:基于上下文的动态关联
自注意力机制的核心思想是:一个词在句子中的含义,是由它与句子中所有其他词(及自身)的关系共同决定的。
让我们看一个经典例子:
“The animal didn’t cross the street because it was too tired.”
在这个句子中,"it" 指的是什么?
- 如果后面是 “it was too tired",”it" 很可能指 “animal” 动物累了)
- 如果后面是 “it was too wide",”it" 就很可能指 “street"(街道太宽了)
自注意力机制就是让模型学会这种动态的、基于上下文的关联。它通过计算 “it” 与句子中所有其他词的相关性分数,从而决定应该从哪些词中"吸收"信息。
3.2 核心组件:Query, Key, Value (Q, K, V)
为了实现上述目标,自注意力机制为每个输入单词(更准确地说是每个词的嵌入向量 Embedding)创建三个不同的向量:
1. Query(查询向量,Q)
- “我要找什么?” 它是当前单词的"代理人”,负责去"提问"
- 比如,当模型处理 “it” 时,“it” 的 Q 向量会问:“嘿,句子里的大家,谁最符合’我’(it)所指代的对象?”
2. Key(键向量,K)
- “我是什么标签?” 它是每个单词的"标签"或"索引",用来被 Query 查询
- “animal” 的 K 向量会说:“我是一个名词,表示动物”
- “street” 的 K 向量会说:“我是一个名词,表示街道”
- “tired” 的 K 向量会说:“我是一个形容词,表示疲惫”
3. Value(值向量,V)
- “我的实际内容是什么?” 它代表该单词的实际语义信息
- 当 “it” 的 Q 向量通过匹配 K 向量,发现 “animal” 是最佳匹配时,它最终"取走"的是 “animal” 的 V 向量
搜索引擎类比
这个过程可以类比为一次网络搜索:
| 注意力机制 | 搜索引擎 |
|---|---|
| Query (Q) | 你在搜索框输入的搜索词 |
| Key (K) | 搜索引擎索引中每个网页的标题/关键词 |
| Value (V) | 搜索引擎返回的网页实际内容 |
查询词(Q)与关键词(K)匹配计算相似度,然后相应的内容(V)被按权重返回。
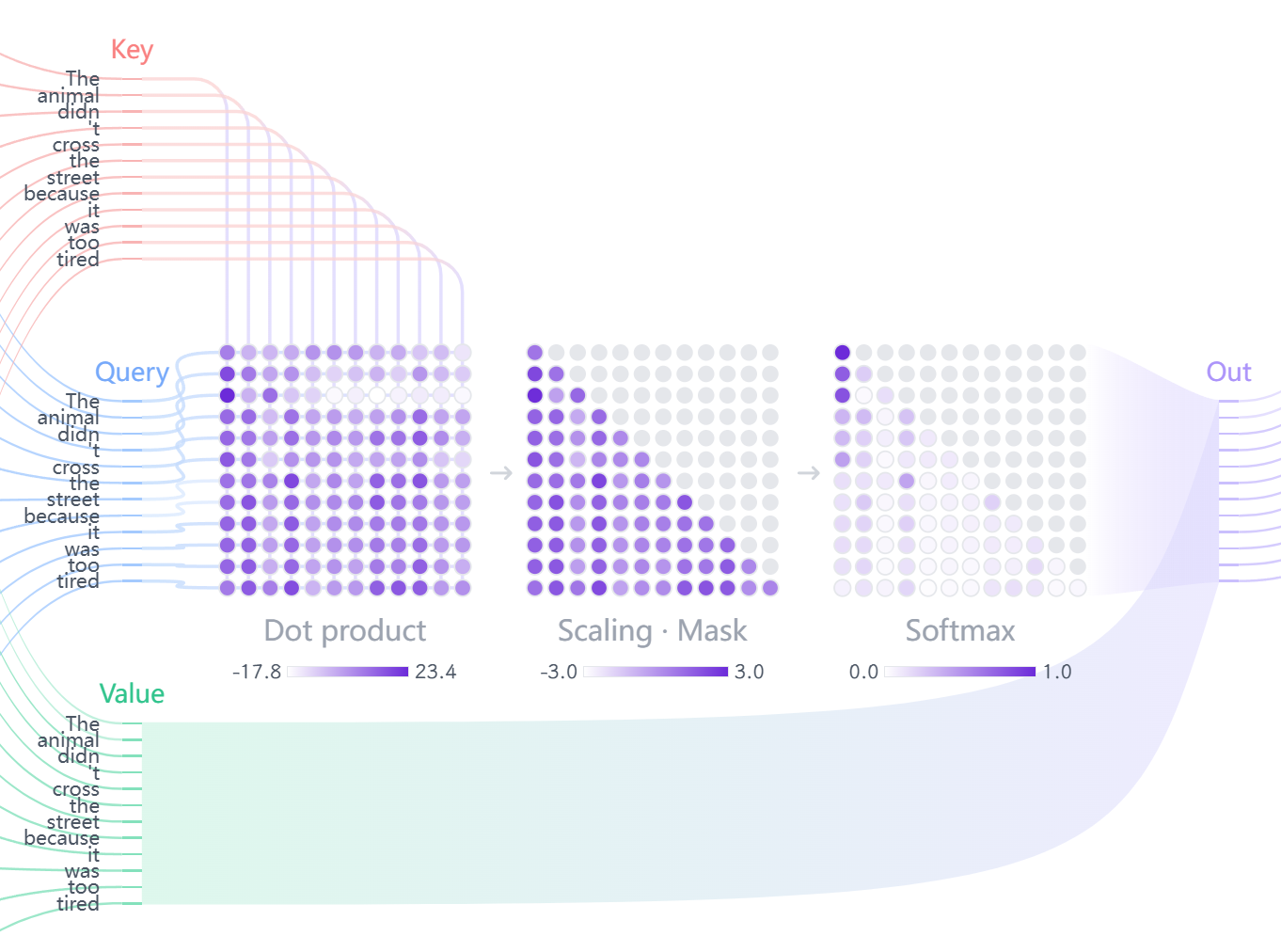
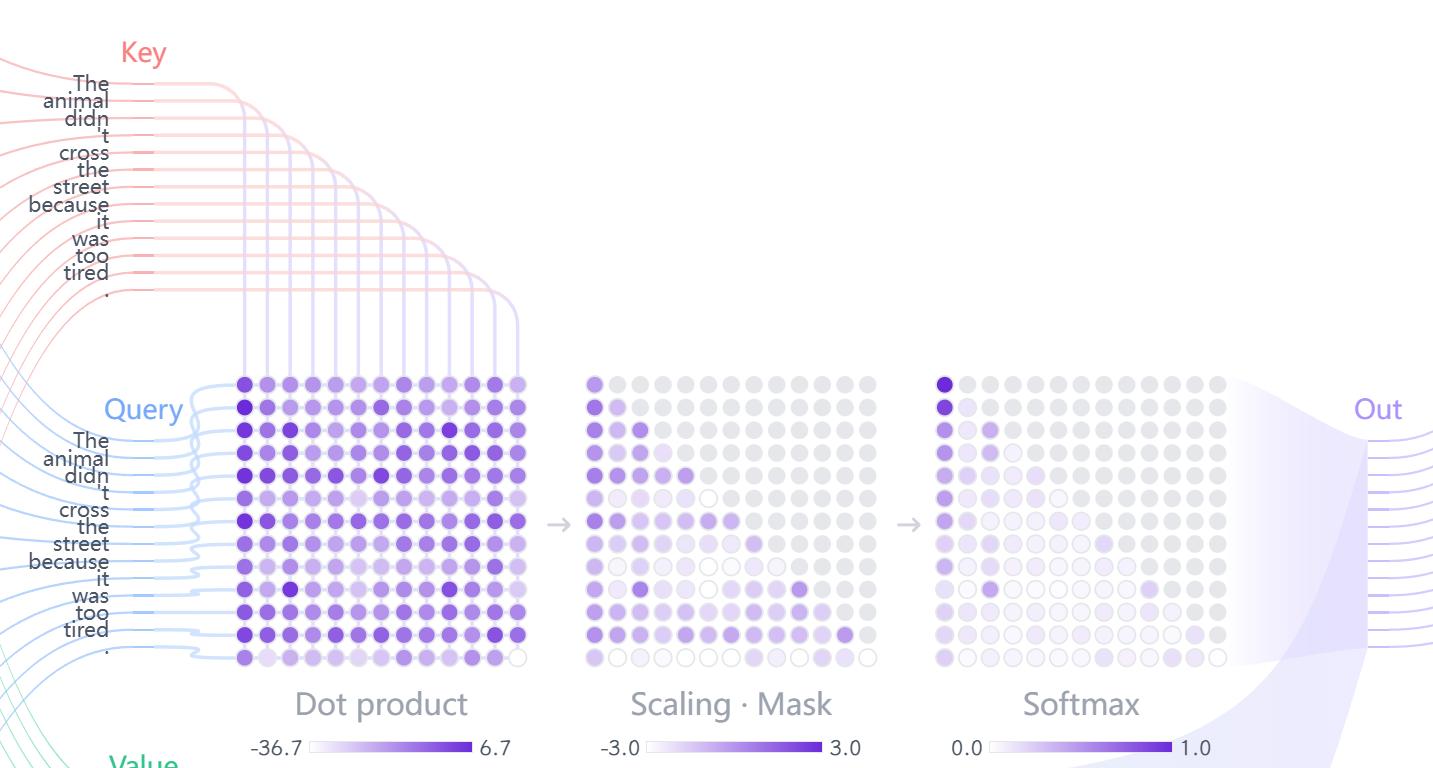
3.3 计算SDPA(Scaled Dot-Product Attention)
现在我们详细看看 “it” 这个词是如何通过自注意力更新自己的表示的。
步骤 1:生成 Q, K, V 向量
假设:
- “it” 的原始嵌入向量是 (x_{it})
- “animal” 的嵌入向量是 (x_{animal})
模型有三组可学习的权重矩阵:(W^Q), (W^K), (W^V)(这三个矩阵在整个句子中是共享的)
通过矩阵乘法生成 Q, K, V:
$$ \begin{aligned} q_{it} &= x_{it} \cdot W^Q \\ k_{it} &= x_{it} \cdot W^K \\ v_{it} &= x_{it} \cdot W^V \end{aligned} $$句子中每个其他词(如 “animal”)也同样生成自己的 K 和 V:
$$ \begin{aligned} k_{animal} &= x_{animal} \cdot W^K \\ v_{animal} &= x_{animal} \cdot W^V \end{aligned} $$根据 Transformer Explainer 的说明,在 GPT-2 (small) 中:
- 输入嵌入维度:768
- Q, K, V 向量维度:64(单个注意力头)
步骤 2:计算注意力分数(Score)
“it”(Query)需要知道它应该给句子中其他每个词(Key)多少关注度。
这个"关注度"通过计算 Q 向量和所有 K 向量的点积(Dot Product) 来得到:
$$ \begin{aligned} \text{Score}(it, it) &= q_{it} \cdot k_{it} \\ \text{Score}(it, The) &= q_{it} \cdot k_{The} \\ \text{Score}(it, animal) &= q_{it} \cdot k_{animal} \\ \text{Score}(it, street) &= q_{it} \cdot k_{street} \end{aligned} $$如果 $q_i$ 和 $k_j$ 向量方向相似,点积值大,说明关联性强
为什么使用点积? 可以参考我的另一篇笔记,详细说明了使用点积进行相似度衡量的原因。
步骤 3:缩放(Scale)
这是 “Scaled Dot-Product Attention” 中 “Scaled” 的来源。将所有分数除以 $\sqrt{d_k}$($d_k$ 是 K 向量的维度,例如 64)。
$$ \text{Scaled Score} = \frac{\text{Score}}{\sqrt{d_k}} $$💡 为什么要缩放?(重要的工程细节)
- 防止 $d_k$ 维度过大时,点积结果过大,导致 Softmax 函数的梯度消失,使训练不稳定。
数学直觉:如果两个独立的标准正态分布随机变量相乘,其方差为 1;如果有 (d_k) 个这样的乘积求和,方差就变成了 (d_k)。因此除以 (\sqrt{d_k}) 可以将方差拉回 1。详细的数学推导可以参考笔记
步骤 4:Softmax 归一化
将缩放后的分数传入 Softmax 函数,得到注意力权重 ($\alpha$)。
$$ \alpha_{i,j} = \text{softmax}(\text{Scaled Score}_{i,j}) $$- 这会将词 $i$ 对所有其他词(包括自身)的分数转换成一个总和为 1 的概率分布。
- 例如,$\alpha_{\text{it, animal}}$ 可能是 0.85,$\alpha_{\text{it, street}}$ 可能是 0.05。
步骤 5:加权求和
使用上一步得到的注意力权重 $\alpha_{i,j}$,对所有词的 Value 向量 ($v_j$) 进行加权求和,得到词 $i$ 的最终输出向量 $z_i$。
$$ z_i = \sum_{j} \alpha_{i,j} \cdot v_j $$这意味着什么?
“it” 的新表示 $z_{it}$ 是一个加权混合体:例如,“it” 的新向量 $z_{it}$ 将约等于: $0.85 \times v_{\text{animal}} + 0.05 \times v_{\text{street}} + \ldots$
- 它 85% 的"内容"来自 “animal” 的语义
- 再加上少量其他词的信息(如 “tired” 贡献了 6%)
通过这个过程,“it” 的向量表示成功地融合了它所指代的 “animal” 的信息,模型"理解"了 “it” 的指代关系。
(实际情况可能更为复杂,尤其是在多层的MHA中,我其实对Transformer这里的注意力可解释分析也挺困惑的)
3.4 论文中的统一公式
上述所有步骤可以合并为一个高效的矩阵运算公式,这正是 Transformer 能够大规模并行计算的关键:
$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$这里 $Q, K, V$ 是矩阵,它们的每一行代表一个词的 Q, K, V 向量。
- $QK^T$:计算出 $(n \times n)$ 的分数矩阵($n$ 是句子长度),一次性完成所有词对所有词的点积(步骤 2)。
- $/\sqrt{d_k}$:对整个矩阵进行缩放(步骤 3)。
- $\text{softmax}(\ldots)$:对矩阵的每一行分别应用 Softmax,得到 $(n \times n)$ 的权重矩阵(步骤 4)。
- $(\ldots)V$:将权重矩阵与 $V$ 矩阵相乘,得到 $(n \times d_v)$ 的输出矩阵 $Z$。矩阵 $Z$ 的每一行就是该词融合了全局上下文的新表示(步骤 5)。
核心优势:
- 并行计算:所有计算都是矩阵乘法,非常适合 GPU 加速。
- 一步直达:任意两个词之间的关联(无论距离多远)都可以通过一次矩阵运算直接计算,解决了 RNN 的长距离依赖问题。
3.5 可视化理解
根据 Transformer Explainer 的展示,自注意力的计算流程可以可视化为:
3.6 小结
自注意力机制(Scaled Dot-Product Attention) 是一个精妙的计算过程:
- Query:当前词要"查询"什么信息
- Key:其他词提供的"标签"
- Value:其他词的实际语义内容
- 通过 Q 和 K 的点积计算相关性
- 通过 Softmax 得到注意力权重(概率分布)
- 用权重对 V 进行加权求和,得到融合了上下文的新表示
关于SDPA的设计哲学,我总结了其三个比较重要的核心支柱,放在另一个笔记里详细讨论了。
这个机制是 Transformer 的心脏,但论文还有一个关键创新来进一步增强其能力:多头注意力(Multi-Head Attention) 。
4. 多头注意力(Multi-Head Attention,MHA)
自注意力(SDPA)存在一个潜在问题:虽然我们在进行softmax之前对点积结果进行缩放,但是softmax归一化依然可能导致只对少数几个词产生上下文关联,而其余的被压制。(如果模型只有一个注意力“头”,它可能只会学到一种类型的上下文关联。)
例如,在处理 “The animal…because it was too tired” 时,这一个头可能学会了 “it” -> “animal” 的指代关系,但可能忽略了 “tired” -> “animal” 的描述关系。
为了让模型能够同时关注来自不同表示子空间的信息,论文引入了多头注意力机制。
4.1 核心思想:并行与融合
多头注意力的核心思想非常直观:
与其进行一次昂贵(高维度)的单一注意力计算,不如将模型($d_{\text{model}}$)的维度拆分成 ($h$) 个“头”(heads),让每个头(在较低维度上)独立地、并行地学习一种上下文关系,最后再将所有头的结果融合起来。
这就像一个专家委员会:
- 单一注意力:一位全科专家试图独自分析所有问题。
- 多头注意力:(h) 位不同领域的专家(例如,一位语法专家、一位语义专家、一位指代关系专家……)并行工作,然后汇总他们的见解,得出一个更全面、更鲁棒的结论。
4.2 MHA 架构:前向过程详解
假设我们的模型中:
- 输入嵌入矩阵:(X) 形状: ($n \times d_{\text{model}}$)
- 头数 (h) (num_heads):例如 8
- 模型总维度 (d_{\text{model}}):例如 512
关键设定:MHA 会将总维度 ($d_{\text{model}}$) 平均分配给 ($h$) 个头。因此,每个头的 Q, K, V 向量维度会变小:
- $d_k = d_{\text{model}} / h = 512 / 8 = 64$
- $d_v = d_{\text{model}} / h = 512 / 8 = 64$ (注意:这里 (d_k) 和 (d_v) 必须相等)
步骤 1:独立线性投影 (Projection)
MHA 不会直接使用单一的 ($W^Q$, $W^K$, $W^V$) 矩阵。相反,它为 ($h$) 个头中的每一个头都创建了一组独立的权重矩阵。
对于第 ($i$) 个头($i \in [1, h]$):
- 查询权重:$W_i^Q \in \mathbb{R}^{d_{\text{model}} \times d_k}$
- 键权重:$W_i^K \in \mathbb{R}^{d_{\text{model}} \times d_k}$
- 值权重:$W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_v}$
模型使用相同的输入矩阵 ($X$),通过这些不同的权重矩阵,为每个头分别计算出 $Q, K, V$ 矩阵:
$$ \begin{aligned} Q_i &= X \cdot W_i^Q \\ K_i &= X \cdot W_i^K \\ V_i &= X \cdot W_i^V \end{aligned} $$形状变化
- $X$ (形状: $n, d_{\text{model}}$)
- $W_i^Q$ (形状: $d_{\text{model}}, d_k$)
- $Q_i$ (形状: $n, d_k$),同理 ($K_i$), ($V_i$)
直观理解:$X W_i^Q$这一步,就是从原始的 512 维空间中,“投影” 出第 ($i$) 个头所关心的、维度为 64 的 “查询子空间”。
步骤 2:并行计算注意力 (Parallel Attention)
现在我们有了 ($h$) 组独立的 $(Q_i, K_i, V_i)$。MHA 会让这 ($h$) 个头并行地执行缩放点积注意力(SDPA) :
$$ \text{head}_i = \text{Attention}(Q_i, K_i, V_i) = \text{softmax}\left(\frac{Q_i K_i^T}{\sqrt{d_k}}\right)V_i $$并行性: 这 ($h$) 次 SDPA 计算是完全独立的,可以在 GPU 上高效并行。
输出: 我们得到 ($h$) 个输出矩阵 $(\text{head}_1, \text{head}_2, \ldots, \text{head}_h)$,每个矩阵的形状都是 $(n, d_v)$。
直观理解:
- $\text{head}_1$ (形状 $(n, 64)$) 可能学会了指代关系。
- $\text{head}_2$ (形状 $(n, 64)$) 可能学会了时态关系。
- …
- $\text{head}_8$ (形状 $(n, 64$)) 可能学会了主谓一致。
步骤 3:拼接 (Concatenate)
模型将这 ($h$) 个头并行计算的结果(它们都是 ($n, d_v$) 形状)在最后一个维度上进行拼接:
$$ \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_h) $$形状变化:
- 输入:$h$ 个 $(n, d_v)$ 矩阵
- 输出:一个 $(n, h \times d_v)$ 矩阵
- 维度恢复:由于 $(d_v = d_{\text{model}} / h$,所以 $h \times d_v = d_{\text{model}}$。
- 拼接后的矩阵形状为 $(n, d_{\text{model}})$,恢复到了模型的原始维度。
直观理解:我们将 8 个专家的 64 维 “见解” 拼接在一起,形成一个丰富的、512 维的 “综合报告”。
步骤 4:最终线性投影 (Final Projection)
最后,这个拼接后的 $(n, d_{\text{model}})$ 矩阵还不能直接作为输出。它会再通过一个最终的线性层(由权重矩阵 $W^O$ 定义),将这个"综合报告"进行一次融合与转换。
输出权重:$W^O \in \mathbb{R}^{d_{\text{model}} \times d_{\text{model}}}$
最终输出 $Z$:
$$ Z = \text{Concat}(\text{head}\_1, \ldots, \text{head}\_h) \cdot W^O $$- 形状:Z 的形状为 $(n, d_{\text{model}})$,与 MHA 模块的输入 $X$ 形状完全一致。这使得它可以被堆叠在 Transformer 的其他层中。
直观理解:$W^O$ 矩阵是一个可学习的“融合线性层”。它学习如何最佳地组合 8 个头的输出。例如,它可能学到:“在决定’it’的含义时,头 1 (指代) 的权重给 0.6,头 5 (语法) 的权重给 0.2,其他头的权重给 0.2…”
4.3 统一的数学公式
上述四个步骤可以被总结为 MHA 的统一公式:
$$ \text{MultiHead}(X) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h) W^O $$其中,每个头 (\text{head}_i) 的计算如下:
$$ \text{head}_i = \text{Attention}(XW_i^Q, XW_i^K, XW_i^V) $$- Attention 函数即为我们上一章定义的缩放点积注意力 (SDPA)。
- $W_i^Q, W_i^K, W_i^V$ 和 $W^O$ 都是模型在训练中需要学习的参数。
4.4 可视化理解与小结
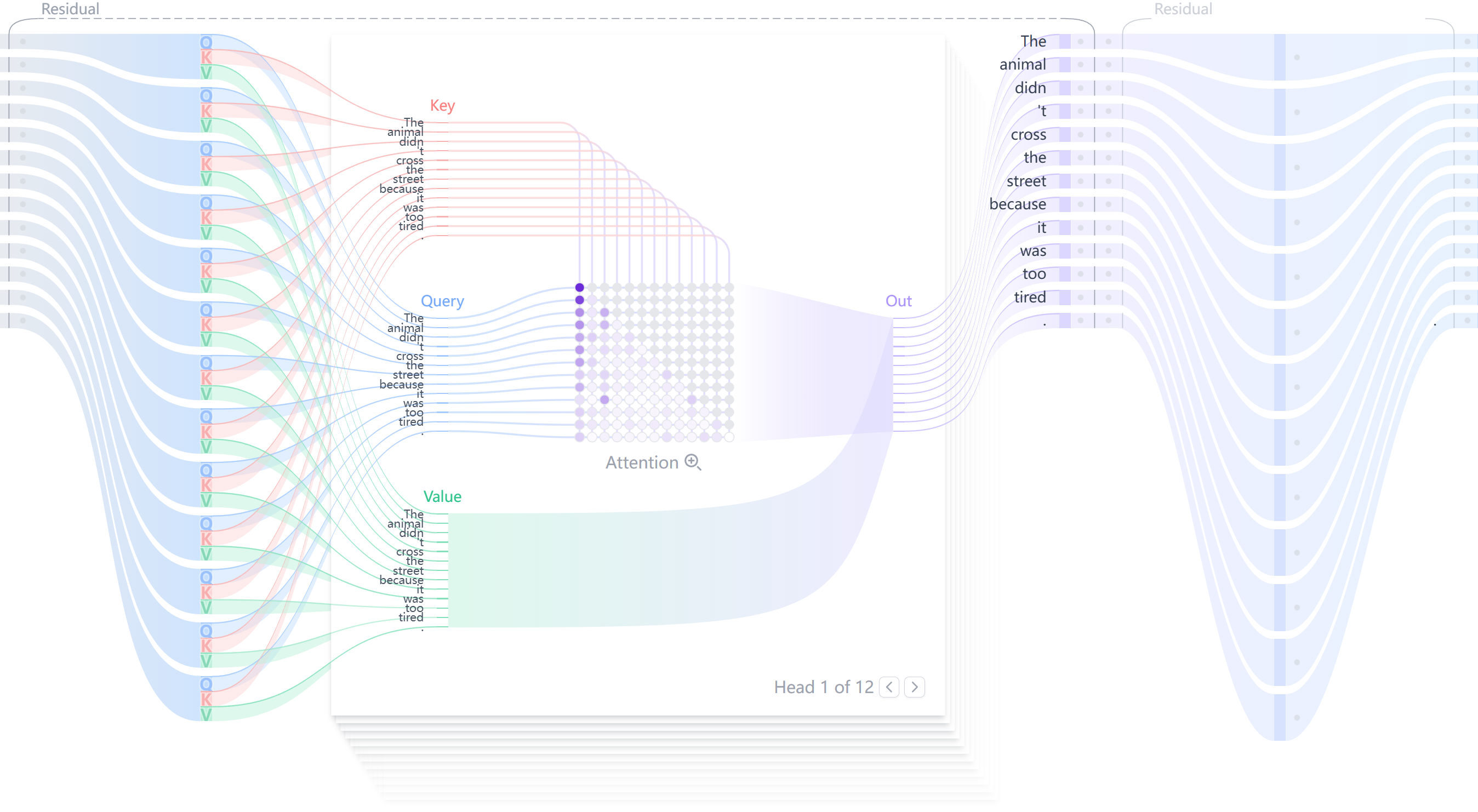
在 Transformer Explainer 网站上,当你在 “Multi-Head Self-Attention” 部分时,你会看到多组(通常是 12 组) 注意力计算的权重矩阵。
MHA 的核心优势:
- 多维视角:允许模型在不同的表示子空间中捕捉不同类型的上下文关系。
- 表达力更强:一个头"算糊了"没关系,其他头可以补偿。
- 并行高效:($h$) 个头的计算完全可以并行化,计算效率高(尽管总计算量略大于单头,但效果提升显著)。
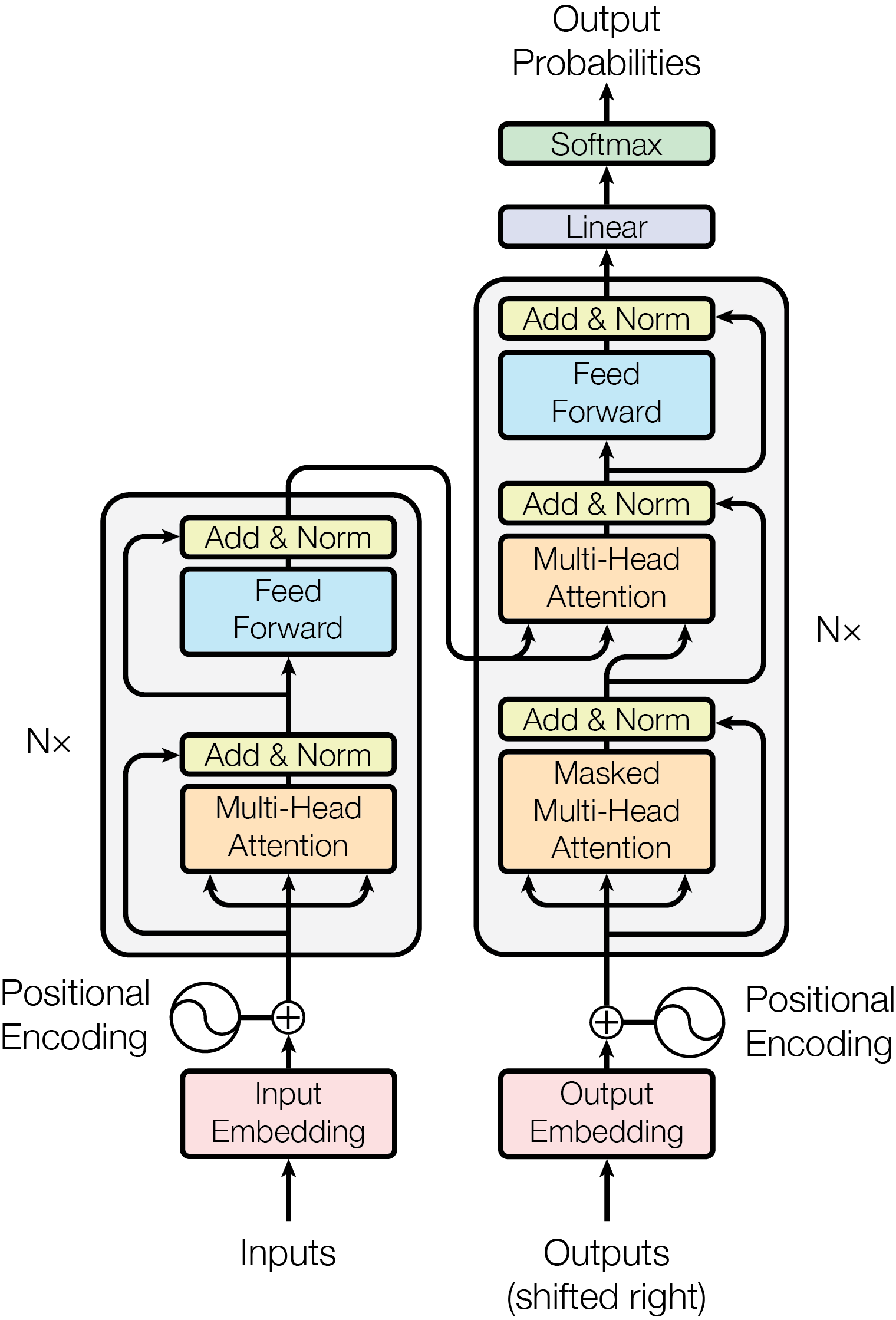
5. Transformer架构
5.1 为什么看到的很多transformer的架构和经典的这张图不一样?
下图是我们最常见也是最熟悉的Transformer架构,它是典型的Encoder-Decoder结构
但是仔细一看不难发现,它和我们在 Transformer Explainer 网站上看到的Transformer结构完全不同,这是什么原因呢?
答案是:
这是Transformer最传统的任务——语言翻译(例如从中文翻译到英语),常见的LLM有三种类型:
- Encoder-Decoder(编码器-解码器) 结构:经典Transformer架构的
- Encoder-only (如 BERT): 只用左边。擅长理解、分类、完形填空
- Decoder-only (如 GPT 系列): 只用右边。擅长接龙、生成文本。Transformer Explainer 通常展示的是 GPT 类的架构,所以只看得到 Decoder
与RNN的关系
5.2 transformer核心组件详解
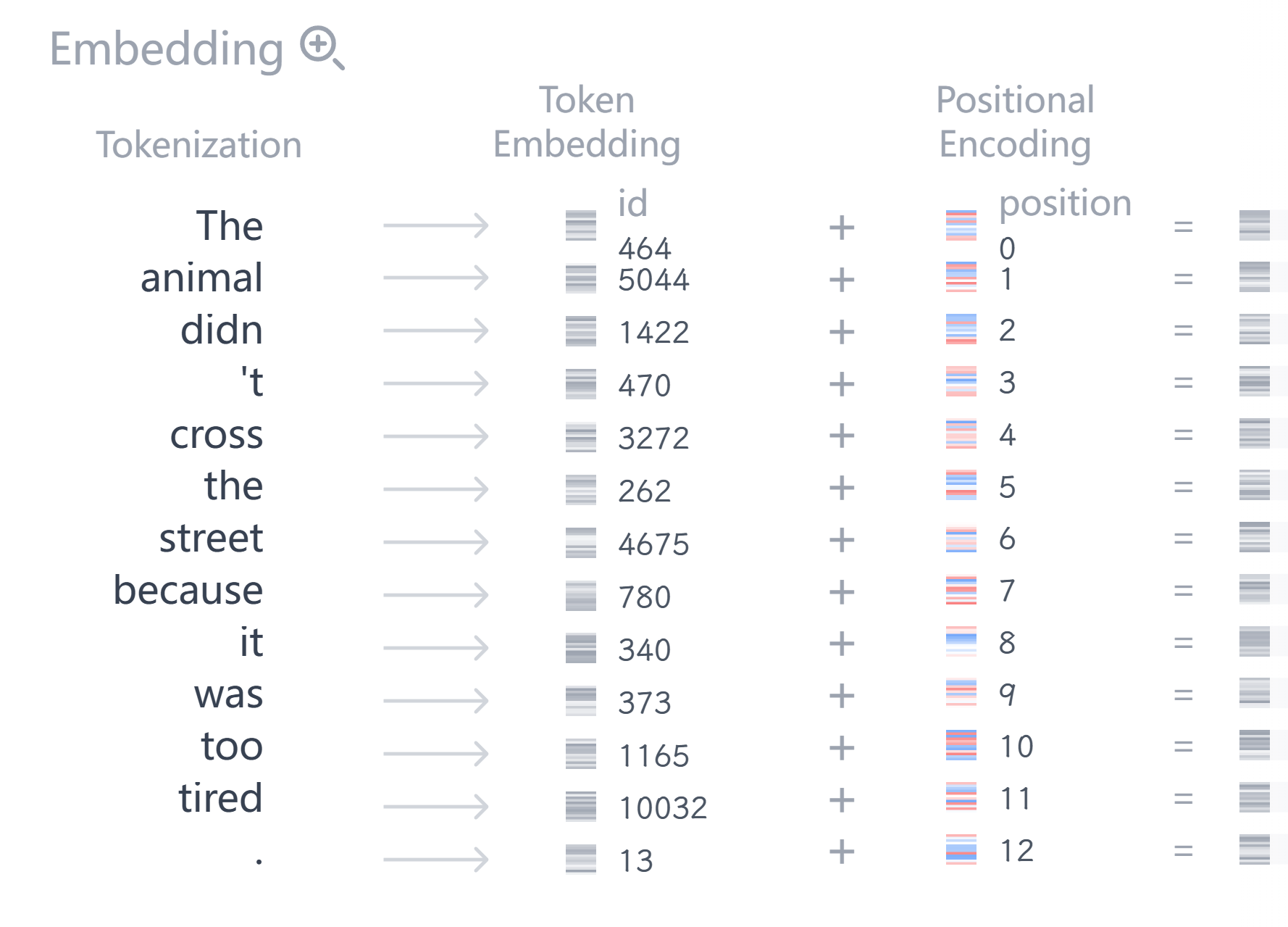
1. Input Embedding
这里是LLM开始的地方,是将人类理解的字符转换为机器理解的数学向量的关键。对于“Apple这个词”计算机可能无法理解这五个字母的组合到底是什么,所以这里涉及两个步骤:
- Tokenization: 将 “animal” 变成一个索引 ID(如图:
5044)。 - Embedding: 将 ID
5044映射到一个高维的稠密向量(例如:长度为 512 的向量)。这个向量代表了该单词的语义。
Embedding的过程和Word2Vec的过程极其相似,但是有重大区别:
Word2Vec:是预训练的静态词向量,在训练完成后就固定不变
Transformer Embedding:是可学习的嵌入层,在模型训练过程中会不断更新优化
如何进行分词?
对于Word2Vec,我们有CBOW这样的方法可以进行向量化。而对于Embedding那你一定会想问:这个ID是怎么确定的?
实际上,这里涉及了一个过程——tokenization
以GPT为例,在正式训练之前,我们先要进需要训练的文本编码成一个“字典”。对于GPT来说,其最主要使用BPE算法(Byte Pair Encoding)简单来说具体涉及以下步骤确实是非常简单的情况,tokenizer的研究其实也非常丰富,可以试想一下其他语言(中文?)的情况。 :
- 一开始只有字母:
a, b, c, ...- 发现 “h” 和 “e” 经常在一起 $\to$ 合并为 “he”。
- 发现 “t” 和 “he” 经常在一起 $\to$ 合并为 “the”。
- 发现 “ani” 和 “mal” 经常在一起 $\to$ 合并为 “animal”。
- 最终我们选出出现频率最高的(例如)50,000 个组合,给它们编号(ID 0:
<pad>,… ,ID 5044:animal)
tokenizer.json 或 vocab.txt如何进行向量化?
这个问题其实就简单了,可以将Embedding理解为一个可训练的参数矩阵,大小为 (vocab_{size}×d_{model} ),即之前tokenizer生成词表的大小以及设定的词嵌入向量维度。这时的标签就可以与矩阵的index对应,形成端到端的训练了,其实在torch中涉及到这样两行代码:
# 输入是离散的 ID (Int)
embedding = nn.Embedding(vocab_size, d_model)
x = embedding(input_ids) #通过tokenizer张量化后的id,比如"animal":torch([5044])
# 此外,如果有预训练词嵌入权重的话,可以直接导入
weight = torch.FloatTensor([[1, 2.3, 3], [4, 5.1, 6.3]])
embedding = nn.Embedding.from_pretrained(weight)
对于VisionTransformer呢?
这个问题其实也比较好回答,首先Vit论文里指出将图像送进Transformer之前也需要进行token化,而图像的token他们选用PatchEmbedding进行处理,简而言之就是将原始图像切块之后对一个图像块(16×16)原始论文使用的大小 进行向量化,我们以最常见的Dino为例,其实就是一个卷积层:
# 简化版
class PatchEmbed(nn.Module):
"""
2D image to patch embedding: (B,C,H,W) -> (B,N,D)
Args:
img_size: Image size.
patch_size: Patch token size.
in_chans: Number of input image channels.
embed_dim: Number of linear projection output channels.
"""
def __init__(
self,
img_size: Union[int, Tuple[int, int]] = 224,
patch_size: Union[int, Tuple[int, int]] = 16,
in_chans: int = 3,
embed_dim: int = 768,
) -> None:
super().__init__()
......
self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_HW, stride=patch_HW)
self.norm = norm_layer(embed_dim) if norm_layer else nn.Identity()
def forward(self, x: Tensor) -> Tensor:
_, _, H, W = x.shape
x = self.proj(x) # B C H W
return x
2. Positional Encoding
为什么需要它?
这是 Transformer 与 RNN 最大的不同点之一。
- RNN: 天然知道位置,因为它是一个接一个读的(读了第一个才能读第二个)。
- Transformer: 这是自注意力的“缺陷”——MHA 本身是一个"集合"(Bag-of-Words)模型。对于 MHA 来说,“The dog bit the man” 和 “The man bit the dog” 没有区别,因为 Q, K, V 矩阵的计算与顺序无关。
因此我们需要赋予这些token一定的序列信息(自然语言),而不同的任务可以需要不同的编码方式,这里先埋一个坑位置编码新坑篇 。
正弦位置编码
Transformer Explainer 这里的可视化非常的简略,对于位置编码只是用0,1,2…进行示意表达(其实这样会有很大弊端),对于 “Attention is all you need” 的原论文,作者探讨了一个位置编码应该拥有的一些优良性质这里参考了知乎大佬的博客解释 :
- 绝对位置标识: 每个位置的token需要有唯一的向量编码
- 相对位置表示: 在序列长度不同的情况下,不同序列中token的相对位置/距离也要保持一致
- 序列长度外推: 可以用来表示模型在训练过程中从来没有看到过的句子长度
原始 Transformer 的位置编码(假设序列位置为 pos、维度为 i):
等价写法:设频率 $\omega_i = 10000^{-2i/d_\text{model}}$,则
$$ \text{PE}(pos) = \big[ \sin(\omega_0 pos), \cos(\omega_0 pos), \sin(\omega_1 pos), \cos(\omega_1 pos), \dots \big] $$这样的设计除了满足上述三个设计需求之外,还有一些优良的性质:
相对位置的线性可表示性与内积的平移不变性
多尺度分辨率与唯一性,类似于构造几何级数的傅里叶基,用于拟合任意关于位置的函数
规范性与数值稳定性,每个位置编码的值域严格限制在 $[-1, 1]$ 之间,数值分布稳定且较小
Noteps. 如果用直接用整数 $1, 2, 3…$ 进行编码,数值会随着句子变长而无限增大,导致梯度爆炸或数值不稳
对于正弦位置编码(Sinusoidal Positional Encoding) 优良性质,打算开一个新的笔记进行解读
3. Add & Norm
它的整体公式是:
$$ Output = LayerNorm(x + Sublayer(x)) $$1. Add: 残差连接 (Residual Connection)
在架构图中,你会看到每个子层(Attention, FFN)后面都与前面连接着一个虚线 Residual Connection。这是训练深层网络的防止梯度消失的重要工具,这个是ResNet中流传下来的方法(这也是为什么ResNet被称为神作的原因)。
- 操作: 将子层的输入 $x$ 直接加到子层的输出上。
- 作用: 防止梯度消失。这就好比在深层网络中搭了一条“高速公路”,让梯度可以无损地流回前面的层,使得深层网络(如 100 层的 GPT-4)能够被成功训练。
2. Norm: 层归一化 (Layer Normalization)
- 操作: 对每一个样本的向量特征维度((d_{model}))进行归一化(减去均值,除以标准差),使其转化为标准正态分布。
- 作用: 稳定神经元的激活值,加速收敛。
- 与 Batch Norm 的区别: Batch Norm 是跨样本归一化(依赖 Batch Size),而 Layer Norm 是在一个样本内部跨特征归一化(独立于 Batch Size),这更适合 NLP 这种变长序列的任务。
4. Point-wise Feed-Forward Networks (FFN)参考博客
在 Attention 层之后,每个 token 的向量虽然聚合了上下文信息,但还需要进一步的“消化”和非线性变换。这就是 FFN 的作用。
结构
它实际上是一个简单的两层全连接神经网络 (MLP)。
$$FFN(x) = \max(0, xW_1 + b_1)W_2 + b_2$$- 第一层: 线性变换,通常将维度放大(例如从 512 放大到 2048)。
- 激活函数: 使用 ReLU 或 GELU(引入非线性能力)。
- 第二层: 线性变换,将维度缩放回原来的大小(例如从 2048 变回 512)。
为什么要叫 “Point-wise”?
这是一个很关键的概念:独立性。
FFN 对序列中的每一个位置(词)是独立且相同地作用的。这其实是很重要的一个概念,正因为 FFN 对位置无能为力,所以我们必须保证 Attention 机制 能够极度完美地处理位置信息,这也是后续对transformer研究中对位置编码进行改进或者使用可学习位置编码的比较重要的原因。
- 比如处理 “I love AI”:FFN 处理 “I” 的参数,和处理 “love” 的参数是完全同一套矩阵,而且处理 “I” 的时候完全不需要看 “love”。
- 上下文信息的交互已经在 Attention 层完成了,FFN 层只负责增强单个词的特征表达能力。
5. Masked Self-Attention & Cross-Attention
1. Masked Self-Attention (带掩码的自注意力)
也叫因果注意力。在训练阶段,Transformer 采用了 Teacher Forcing 模式。这意味着我们将完整的正确答案(例如 “I love AI”)一次性喂给 Decoder。
- 如果不加 Mask: 当我们预测第一个词 “I” 的时候,Self-Attention 机制允许模型“看见”后面的 “love” 和 “AI”。这就像考试时把答案摆在旁边,模型会直接抄袭后面的词,而不是去学习如何根据上文预测下文。这会导致推理(Inference)时彻底失效,因为推理时是没有后面单词的。
- 加了 Mask: 我们要强制模型遵循因果关系 (Causality):在预测第 $t$ 个词时,只能看见 $t$ 之前的信息,绝对不能看见 $t$ 之后的信息。
怎么实现?($-\infty$ 矩阵)
如上图所示,在计算 Attention 分数之后、Softmax 之前,加上一个掩码矩阵。
$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}} + M\right)V $$其中 $M$ 是一个下三角矩阵(Upper Triangular Matrix)。
操作图解
假设句子长度是 4。
未 Mask 的 $QK^T$ 矩阵(4x4)代表每个词对其他词的关注度。我们要把右上角(未来信息)全部屏蔽。
生成掩码矩阵 $M$:
黄色部分设为 $-\infty$(负无穷大),白色部分为 0。
$$ M = \begin{pmatrix} 0 & -\infty & -\infty & -\infty \\ 0 & 0 & -\infty & -\infty \\ 0 & 0 & 0 & -\infty \\ 0 & 0 & 0 & 0 \end{pmatrix} $$应用 Softmax:
我们知道 $e^{-\infty} \approx 0$。
经过 Softmax 后,矩阵变成了:
$$ \text{Weights} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ \alpha & \beta & 0 & 0 \\ \gamma & \delta & \epsilon & 0 \\ x & y & z & w \end{pmatrix} $$- 第 1 行(Word 1): 只能关注自己(Word 1)。
- 第 2 行(Word 2): 只能关注 Word 1 和 Word 2。
- 以此类推…
结论: 通过这种数学技巧,我们在并行计算(一次输入整个句子)的同时,保留了序列的时间顺序特性。
这里在transformer中一般只有Decoder会有这种Masked Attention,我们可以思考一下为什么?
假如在一个翻译任务中,Encoder也被加上了因果注意力,那么就会产生这样的问题,比如:
“The bank of the river. ”
如果加上了Masked Attention,那么在原文理解上,就没有上帝视角了,bank 看不到后面的 river,因此在语义理解上就可能出现问题——这个 bank 到底是“银行”的意思还是“河岸”?但如果有全局上下文,我们就能理解到这句话指的是“这个河流的河岸”,来精准捕获这句话的语义。
2. Cross-Attention (交叉注意力)
为什么需要它?(连接原文与译文)
在原文中,这是 Transformer 真正的 “翻译” 环节。
- Decoder 刚刚通过 Masked Self-Attention 整理好了 “我现在已经翻译出来的半句话” Target)。
- Encoder 手里紧握着 “源语言句子的完整语义” (Source)。
- Cross Attention 的作用就是:拿着手里的半句译文,去源语言里找对应的线索。
核心机制:Q, K, V 的来源差异
这是cross-attention的重点,也是最容易混淆的地方。请务必记住:Q 来自 Decoder,K 和 V 来自 Encoder。
$$ \text{CrossAttention}(Q_{dec}, K_{enc}, V_{enc}) $$首先,V 我们可以唯一确定,它只能来自Encoder,因为MHA的输出的语义内容就是 V,QK只用来计算注意力分数。而对于Decoder,它的目标是完成自回归任务,并没有上帝视角的全局语义信息。(难道你指望从‘I love’两个词中查询出代表‘apple’语义的词吗,这显然不可能)
其次,我们可以这样想,当我的Decoder输入了一段已经翻译好的文字时,比如 “I love” ,这时的 Q 即为 “I love”(经过Masked Attention之后)想要查询的下一个词的信息。而 K 为Encoder的输出结果,即”我爱苹果“经过Encoder编码之后输出(表述原句子的语义编码)。这时 Q”I love“ 会去查询 K “我爱苹果”,注意力分数会分析出,“I love”这个词就是“我爱”,它们的注意力分数很高,下一个词一定不是这两个,于是从 Q 中给到的下一个词的查询结果K 是 “苹果”,并给出其对应的语义 Value。
最终在拿到 “苹果”的语义后,后续的FFN等操作会继续将其进行“翻译”预测为英文“apple”。但其实仔细想这个过程,我们会有两个问题:
一是为什么K、V总是同时出现,为什么会被“绑定”?
这里可以从两个角度进行解释。
逻辑上
类似于一种”隐喻“,K、V原本设计就是键值对(Key-Value)映射
Key 的作用: 是为了被查找。它代表了信息的“特征”或“地址”
Value 的作用: 是为了被提取。它代表了信息“本体”
而 Query自然是查询的信息(类似搜索词)
数学上 我们从SDPA的公式上可以发现:
$$ > \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{Q \cdot K^T}{\sqrt{d_k}}\right) \cdot V > $$第一步:计算注意力图 (Attention Map)
假设 $Q$ 有 $N$ 个词,$K$ 有 $M$ 个词。
$$ > \underbrace{Q}_{N \times d} \cdot \underbrace{K^T}_{d \times M} \rightarrow \underbrace{\text{Scores}}_{N \times M} > $$这个 Score 矩阵 ($N \times M$) 的含义是:Query 中的每一个词,对 Key 序列中 $M$ 个词的关注程度。
第二步:加权求和
$$ > \underbrace{\text{Scores}}_{N \times M} \cdot \underbrace{V}_{M' \times d_v} > $$矩阵乘法规则要求:左矩阵的列数必须等于右矩阵的行数。
即:$M$ (Key 的序列长度) 必须等于 $M’$ (Value 的序列长度)。
所以,总结一下Cross-Attention中的QKV
Q是需要获取信息的一方,K、V是提供信息的一方,比如:
- 在transformer机器翻译任务中:Q 是Decoder出来的当前的单词,K、V是原文。
- 在多模态VQA:Q 是文本问题,K、V是Image Encoder出来的图像特征
- 生成式任务中:Q 是生成的图像编码后的特征,K、V是原始文本
二是Decoder是怎么启动的,即最开始的词是怎么翻译(生成)出来的?
这里其实隐含着两个问题,如果我们仔细盯着transformer的架构,就会发现这样的问题:
- 当Decoder没有词输入的时候,transformer怎么启动?
- 当输入变长了,输出序列是不是也变长了?那怎么只拿一个词?
这里就不得不提到NLP任务中的一个工程化实践了—— “冷启动” 博主是学cv的,这些都是接触NLP任务时的一些困惑
在 NLP 领域,我们会在词表中定义一些特殊 Token (Special Tokens)。其中最重要的一个就是:
<SOS>(Start Of Sentence)- 或者叫
<BOS>(Beginning Of Sentence)在训练时,因为我们已经有了标准答案(Ground Truth)“I love apple”,我们不需要等模型一个字一个字猜。
我们会构造这样的输入输出对:
Decoder 输入 (Input) 期望的输出标签 (Target Label) 含义 <SOS>I 给个开始信号,你要预测第一个字 <SOS> Ilove 给你前缀,预测第二个字 <SOS> I loveapple … <SOS> I love apple<EOS>句子结束了,预测结束符 再者,我们观察上述的流程,因为在 Decoder 中我们使用的是因果注意力,所以后面输入的词完全不会影响前面输入词的前向结果。比如,当输入
<SOS> I的时候,对<SOS>做Masked Attention和Cross-Attention,以及FFN、Layernorm等操作的输出结果与单独对<SOS>的计算一模一样(这里可以回顾上文对transformer架构的介绍)。因此诞生了两个关键的东西:
- 预测时只用取最后一个词的输出embeding即可
- KV Cache,即对Decoder进行自回归的时候,我们可以缓存前面推导过程中历史的 KV 计算结果,每次只用新计算加进来的那个词的QKV即可。
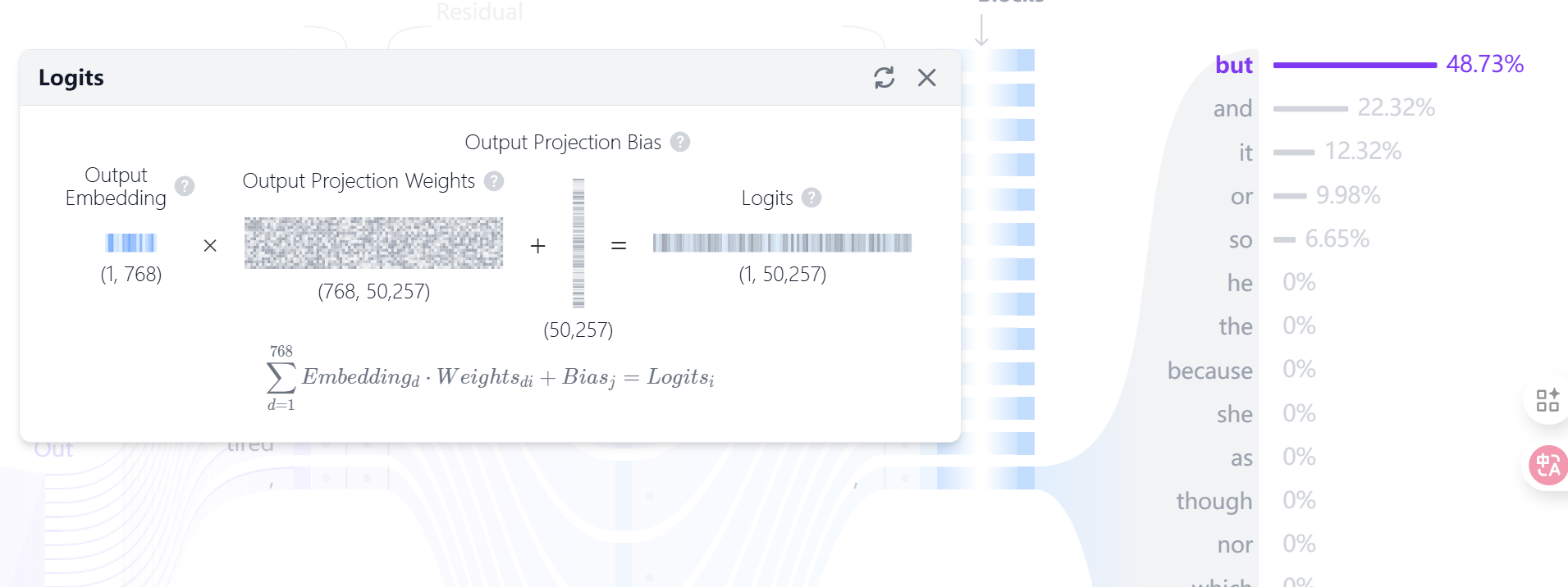
6. Output Logits
Decoder 的输出是一个维度为 $d_{model}$ 的向量(如下图的 768 维)。 我们需要把它映射到词表大小 (Vocab Size)(例如GPT2的 50257 个词)。
这就需要一个全连接层(Linear Layer),它的权重矩阵 $W$ 大小是 $[d_{model}, \text{Vocab_Size}]$。
$$ \text{Logits} = v_{final} \cdot W $$这个输出的长为50257的Logits代表模型对该ID下单词的打分,后续经过softmax等操作可以进一步转化为概率。transformer explainer的示例中有两个模式——Top-k和Top-p,Top-k就是将scale之后的Logits进行排序后去前k个,而Top-p就是上面说的经过softmax转换为概率后取前p个。比较好奇的一点是,这里GPT2的输出竟然不是概率最高的but。
Gemini老师给出的解释是:
这里经历了三个步骤:
Top-p 筛选:如上所述,系统圈定了一个候选池
[but, and]。Normalization (重归一化):
因为砍掉了后面的词,现在的概率加起来只有 $0.38 + 0.18 = 0.56$,不到 100%。
必须把它们放大,重新变成 100%。
计算 and 的新概率:
$$\frac{0.18}{0.38 + 0.18} = \frac{0.18}{0.56} \approx 32.1\%$$(图虽然显示 31.42%,可能是精度差异,但逻辑就是这个比例)。
此时,
but的新概率约为 68%,and的新概率约为 32%。Sampling (最终抽样):
- 系统拿着这两个新概率掷骰子。
- 虽然
but面大(68%),但骰子正好落在了 32% 的区域。- 于是,模型最终输出了 “and”。
确实,当多运行几次后出现“but”的概率还是比较大的。

评论